何年も前、深夜TV番組ロケで、大きな送風機を抱えて、スカート姿に風をあてて、スカートがめくれやすい条件を調べる実験をしたことがあります。さまざまな種類のスカートに、（手で持った送風機で）さまざまな風のあて方をする…という実験を延々２時間以上しましたが、スカートを風でまくり上げるのは意外なほど難しいものでした。
しかし、送風機の風でスカートをまくり上げるのが難しかったのは、風を横からあてていたからで、スカートの下から強風を送れば、もちろん一瞬でスカートは吹き上げられてしまいます。それはつまり、「下から風が吹くような場所」ではスカートが風でめくれやすい、ということです。スカートは、種類によって違いますが、およそ１００〜３５０グラム程度の重さです。そんな重さのスカートを持ち上げることができる程度の風が、スカートの下方向から吹けば、風によってスカートはめくれあがってしまうことになります。
「下方向から風が吹く」場所として、地下鉄駅のホームに降りるエスカレータがあります。地下鉄のホームに列車が近づいてくる時には、駅に近づいてくる列車が空気を圧縮し・ホーム近くの気圧を高めるため、ホーム側から（上部フロアに向かう）階段・エスカレータ通路で、上部フロアに向かう風が吹きます（参考：地下鉄の風）。この「列車風」と呼ばれる風は、条件によって異なりますが、たとえば風速5m/s程度になることがあります。それでは、スカートの下方向から吹く風速 5m/s の風がスカートをめくり上げることができるのでしょうか？
非粘性流体のエネルギー保存則であるベルヌｰイの定理を使うと、スカート下部から吹く風が「スカートを持ち上げようとする力」は、
空気の密度 × スカートに下部から風が吹き込む面積 × 風速 × 風速 / 2
で見積もることができます。空気の密度を1.13(kg/m^3)として、スカートに下部から風が吹き込む面積は（ヒップ90ｃｍの女性で見積もると）0.06(m^2)程度でしょう。そして、ホームに向かうエスカレータに吹く列車風が5(m/s)とすると、
「スカートを持ち上げようとする力」=1.13× 0.06 × 5 × 5 / 2 = 0.85 (N)
になります。0.85 (N = ニュートン)ということは、0.85 (N) / 0.98 = 0.86kg重＝86グラムのものを持ち上げるのと同じ大きさの力ということですから、重さ８６グラムのスカートであったなら、ホームに向かうエスカレータ通路に5m/sの列車風が吹くとスカートがめくれあがってしまう、ということになります。とはいえ、スカートの重さは、冒頭に書いたように１００〜３５０グラム程度ですから、重さ８６グラムのスカートは「素材が非常に薄く軽い特殊なスカート」ということになります。だから、普通のスカートであれば、この程度の風では、スカートがめくれる可能性は低いわけです。
しかし、スカート女性がエスカレータを急いで電車に乗ろうと駆け下りていたりすると、話は大きく変わります。たとえば、女性がでエスカレータを駆け下りていて、下りエスカレータ速度と駆け下りる速度が加わり（下りの速度が）秒速1m程度になった場合には、この1m/sが風速（5m/s）に足し合わされることになり、
「スカートを持ち上げようとする力」=1.13 × 0.06 × (5+1) × (5+1) / 2 = 1.2 (N) = 0.12 kg重
となり、重さ120グラム程度の（結して珍しくはない）スカートがめくれあがってしまうようになるのです。
ちなみに、空気の密度は「高気圧で気温が低くて湿度が低い」時に重くなります。たとえば、１気圧・気温40 ℃・湿度0%の空気の密度は1.13 kg/m^3ですが、気温が0°まで下がると、密度は1.29 kg/m^3になります。また、気圧が5%高くなれば密度も5%高くなります。…そうした条件がすべて加わると、つまり「涼しく晴れた高気圧の温度が低い朝の地下鉄駅で、下りのエスカレータを（遅刻をしまいと）ドジっ娘が駆け下りる」状況で計算すると、
「スカートを持ち上げようとする力」=1.29 × 0.06 × (5+1) × (5+1) / 2 × 1.05 = 1.5 (N) = 0.15 kg重
となり、重さ150グラム程度の平均的な薄手スカートがめくれあがってしまう！ということがわかるのです。
さらに言えば、列車風は「上り・下りの両ホームに同時に列車が進入してきて、その列車がどちらも（その駅には止まらない）通過列車だった」という時に、最大風速を記録しそうです。ということは、駅に止まらない通過列車がある地下鉄副都心線の（大きくない）駅などが、エスカレータ通路にスカートがめくれやすい風が吹く「スカートめくれの危険スポット」ということになります。
計算してみると色んなことがわかる！というわけで、今回は「風でめくれるスカート」を科学してみました。「涼しく晴れた朝の地下鉄駅をドジっ娘が走る」とスカートが必ずめくれる!?くらいの力が生じてしまうのです。
ツール・ド・フランス 2013が開幕しました。6月29日〜7月21日の約3週間をかけて、山あり谷ありな約3,400kmを走り抜く、フランスで開催される自転車レースです。
ツール・ド・フランスに関するビデオを観ていると、このレースを走り抜くために必要なエネルギー量を試算した結果が示されていました。コースが日によって違うため、もちろん日によって必要エネルギー量は変わりますが、平均6750 kcal/日でトータル141666 kcalだというのです。…今回は、この選手達が行う運動の量を「実感」してみることにします。（関連資料：小島よしおのツール・ド・フランスに挑戦！）
たとえば、昨年のツール・ド・フランスの優勝タイムは87時間34分47秒です。
この時間で、トータル141666 kcalの運動を選手たちがしたということは、選手たちの仕事率（時間あたりに行った仕事量）を計算すると1880 ワットに相当します（80W程度の基礎代謝分は含まない計算です）*。
———————————–
追記* …このトータル141666 kcalは「消費カロリー」で、最終的に選手が「自転車を走らせる」ために使われるエネルギー量ではありませんでした。
人の身体の熱効率がどこかで抜けてるんじゃないでしょうか。今の競技用自転車には出力計なるものを装備する事が可能で、それによるとツールドフランスに出場するレベルの選手が1時間持続可能な出力は350W程度とされています。
@ma_molさん
つまり、選手の筋肉が行った仕事の4/5くらいは「自転車を漕ぐ」ためには使われていない…ということのようです。
———————————–
この1880 ワットは一体どのくらいのものかというと、たとえば私たちの身の回りにあるエアコンで言うと、ちょうど４０畳用くらいを冷やす能力があるエアコンが使う電力に相当します。つまり、自転車に発電機を取り付けた「自転車発電機」にツール・ド・フランス選手を乗せて、レースのごとく頑張ってペダルを回してもらえば（申し訳なくも”冷やしたい部屋”の外側で…）、４０畳エアコンを動かし続けることができる、というわけです。自転車発電は、実際やってみると１００Wくらいでも結構大変ですが、選手たちはその20倍近く可能…というのは何だか信じられないくらいの数字です。
———————————–
追記* …「選手たちはその20倍近く可能…というのは何だか信じられないくらいの数字」なのも当たり前で、「ツールドフランスに出場するレベルの選手が1時間持続可能な出力は350W程度」ということですから、「普通の人の６倍くらいの凄さ」ということになります。それでも、十分すごいものですね。
———————————–
そして、この運動を支える１日平均6750 kcal のエネルギーは、
ラーメン二郎の大ラーメン３杯分に相当します。…つまり朝昼晩の３食ともラーメン二郎でガッツリ食べなければならないくらいの運動を、ツール・ド・フランスの選手たちはしているということになります。
朝昼晩にラーメン二郎の大を食べ、（５人いたら）４０畳エアコンを動かし続けることができるツール・ド・フランス選手…凄いですね。
知識検索エンジンWolfram Alphaは、有名人や有名キャラクターたちの顔や姿といったさまざまな画像を「手書きイラスト風の曲線(数式)」にすることができます。それは、顔や姿を描く線を三角関数をパラメータとして表現するフーリエ記述子と呼ばれるテクニックで実現されています。（参考：「初音ミクやアラレちゃんを描く曲線」を作るテクニックの秘密、検索エンジン Wolfram Alpha が作り・表示する各種の「曲線」の裏側）
フーリエ記述子で描画線を表した場合、言い換えれば曲線のパラメータをフーリエ級数で表現した場合には、鋭く曲がる線は苦手(高次数までのたくさんの項が必要とされる)です。そこで、「Wolfram Alpha同様のフーリエ記述子テクニックを使って、鋭い顔・姿を描くと果たしてどうなるか？」を試してみることにしました。…モデルは、もちろん世界一の鋭利な顔を持つ”カイジ”です。
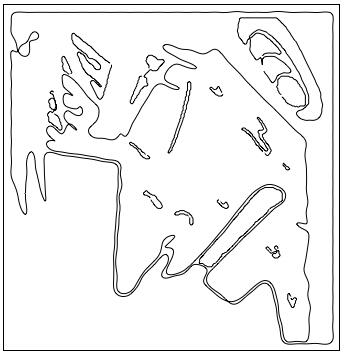まずは、贅沢に１８０次の高次項まで使い、フーリエ記述子で表現してみたのが、この１８０次”カイジ”です。勝負の緊張・不安に襲われてはいるようですが、
止め処ない不安。
底知れぬ恐怖。
…オレは、それでも考え続ける！
的なカイジです。
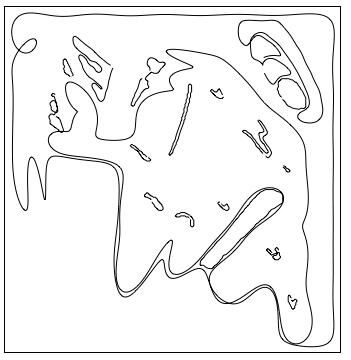さて次は、５０次項までで表現したカイジです。持ち金ならぬフーリエ級数の使用次数が足りなくなってくると、かなりプアー(貧しく乏しい)なカイジになっています。
…オレは！
どこでオレは間違えた？
限りない不安の嵐に押し潰れそうだ…！
なカイジです。
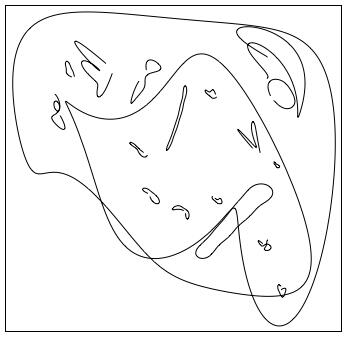
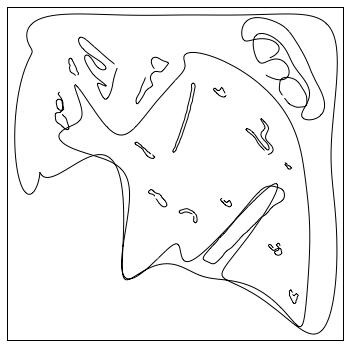そして、最初の約１／１０、２０次項までで描かれた２０次カイジは…もう勝負も決し、カイジの中で何かが崩れ落ち・顔面が溶け始めています。そそり立ち鋭かったはずの鼻も、なんだか鼻高ガイジンさん変装グッズみたいです（あと、しりあがり寿のテイストも12パーセントくらい混じってます）。
さらに（その右に貼り付けた）８次項までだけの8次カイジは、かすかに自慢の鋭利な鼻の片鱗がありますが、もうカイジには全然見えません。しかし、それと同時に、何だか現代美術の巨匠がサラサラと描いた…と言われても納得しそうなモダンアートな8次カイジになっています。
このカイジを「さらに進化させた」のが、４次項までの４次表現カイジです。ここまで低次のみになると…もう、これは原始生物かエンドウ豆か何かにしか見えません。太古、すべての人類は、こんなミジンコ類似な生物の子孫だったのだ！的なカイジです。…いや、もうカイジではないですし、 これは「さらに進化させた」どころか「果てしなく退化させた／先祖返りした」状態です。金ならぬフーリエ表現次数が減ると…もう人間ですらないのです…。
ギャンブルを打つ者にとって
金は寿命！
博黙示録カイジ 1巻
そして最後が、右に貼り付けた、1次の項だけで表現した単純１次のカイジです。「元始、全人類・全てのものは原子であった」的な存在になっています。…しかし、よくよく眺めると、こんな単純な存在まで遡っても、カイジ自慢の鋭い鼻の片鱗が残っていることが凄い！的なカイジです（もうすでにカイジじゃないですが…）。
…こんな風に、マンガの図柄を数式で表された曲線にしてみると、マンガ化の絵柄の違いがわかって面白いかもしれません。たとえば、カイジは１８０次まで必要だけど、丸っこい絵柄の手塚治虫は１０次までで十分だとか、ドラえもんは３次で十分だけど、スネ夫は（特に頭部は）８０次の高次の項まで必要だとか…そんなマンガ図柄の特徴が見えてくるかも？…しれませんね。
