201305.03
「初音ミクやアラレちゃんを描く曲線」を作るテクニックの秘密
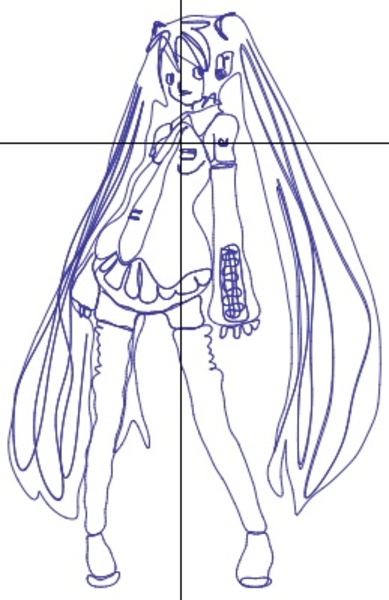 「フィールズ賞はもらった!:初音ミクの数式が解明 さらにいろんな「俺の嫁」が関数で描けることが判明」という記事を読みました。記事内容は、(数式処理ソフトMathematicaの開発元である)Wolfram researchが提供している知識検索エンジンWonfram Alphaが、信じられない図柄、たとえば初音ミクの姿や(Dr.スランプの)アラレちゃんなどの図柄を描き出す「曲線数式」を、次々と作り出すことができる、というものです。
「フィールズ賞はもらった!:初音ミクの数式が解明 さらにいろんな「俺の嫁」が関数で描けることが判明」という記事を読みました。記事内容は、(数式処理ソフトMathematicaの開発元である)Wolfram researchが提供している知識検索エンジンWonfram Alphaが、信じられない図柄、たとえば初音ミクの姿や(Dr.スランプの)アラレちゃんなどの図柄を描き出す「曲線数式」を、次々と作り出すことができる、というものです。
実は、こうした曲線数式は、「フーリエ記述子」という技法を使って自動・単純作業から簡単に作り出すことができるものです。ちなみに、「フーリエ記述子」というのは、たとえば次のようなテクニックです。
まず、数式に変換したい図柄を「(その図柄を描く)曲線の集まり」として分解します。たとえば、もしも図柄が(曲線の集合として表現される)ベクター・グラフィックスでしたら、そのファイルを読み込むだけで、「(その図柄を描く)曲線の集まり」になりますし、あるいは濃淡の画像であれば、たとえば、濃淡の度合いに応じた等高線を描き、その等高線を曲線として考えれば、「(その図柄を描く)曲線の集まり」とすることができます。
次に、それらの曲線(群)を「パラメータで表される曲線」と考えます。たとえば、曲線を各部分での方向(角度)変化という「パラメータの列(集まり)」で表すこともできます。…たとえば、そんな風に、曲線を「パラメータ列」で表現される曲線だと考えてみるのです。
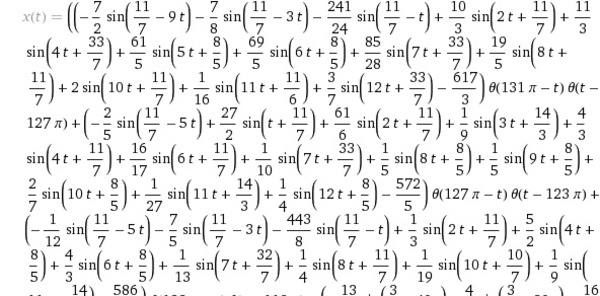 すると、そんなパラメータ列をフーリエ変換することができます。つまり、高校か大学教養あたりで学ぶ、「任意の周期関数は、三角関数を足し合わせとして表現できる」というフーリエ変換を使えば、ありとあらゆる(任意の図柄を表現する)曲線を描くパラメータ列を三角関数の足し合わせ(フーリエ級数)として表すことができます。…これが、図形のフーリエ記述子による表現テクニックです。
すると、そんなパラメータ列をフーリエ変換することができます。つまり、高校か大学教養あたりで学ぶ、「任意の周期関数は、三角関数を足し合わせとして表現できる」というフーリエ変換を使えば、ありとあらゆる(任意の図柄を表現する)曲線を描くパラメータ列を三角関数の足し合わせ(フーリエ級数)として表すことができます。…これが、図形のフーリエ記述子による表現テクニックです。
最後に、フーリエ変換によりさまざまな三角関数の足し合わせにより表現された(図柄を描く)曲線群を、低次の三角関数だけで表してしまえば(高次の三角関数を省略すれば)、高周波数成分が消えることで滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になります(数式も当然短くなります)。あるいは、高次の項(高周波数の三角関数)まで使えば、微細な模様までも描き出すリアルな曲線を得ることもできます。こういった作業は、単純な数値演算により自動で行うことができます。

…実際、Wolfram Alpha上で「(さまざまな図柄を表示するための)曲線の数式」を眺めてみれば、それらはすべて「三角関数の足し合わせ」で表されていることがわかります(つまり、数学的には、実際のところ、それほど美しいものではありません)。これらが、知識検索エンジンWolfram Alphaが作り出す「さまざまな曲線数式」の作りテクニックの秘密です。
 ——————————–
——————————–
関連記事:■Wolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピ
「フーリエ記述子で表現された数式」は美しい存在ではありませんが、(多種多様な存在を単純で良い性質を持つ三角関数の集まりへと分解する)フーリエ級数は実に単純かつ美しい(そして現在のテクノロジーをありとあらゆる分野で支えている何より便利な)存在です。…もしも、教科書の中、目次や頁の先に、「フーリエ級数」なんて項目を見つけたら、その美しさと便利さに感動すること間違いありません。

