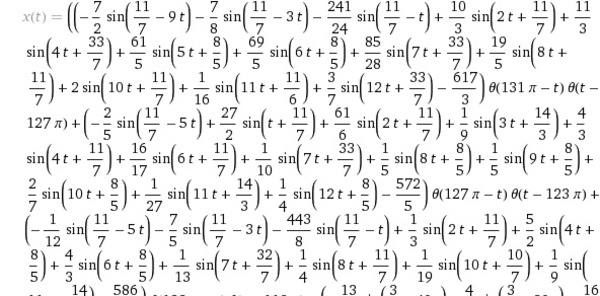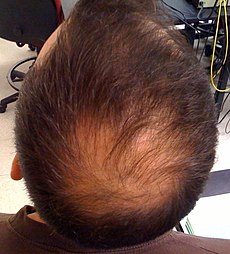
髪の毛が薄くなってくると、髪の毛の隙間から頭の地肌が見えるようになり、いわゆる「ハゲかかってる」と人から呼ばれる状態になります。あなたが、もし薄毛に心を痛めていたとして、あなたの前に「薄毛(ハゲ)の神様」が現れ、「おまえの悩みはわかった!よし、おまえに、毛髪の本数を2倍にするか、あるいは、太さを2倍にするかのどちらかを選ばせてやろう!さぁ、どうする!?」と宣言したとしたら、あなたなら、薄毛改善のためにどちらを選ぶでしょうか?
実は、薄毛改善のためには、毛髪の「多さ」を増やすよりは、「太さ」を増やす方がずっと効果的なのです。下の2枚のグラフは、「毛髪の太さ」と「毛髪本数」に応じた「髪の毛の隙間から頭部地肌が透けて見える度合い」を計算してみたものです。左下グラフは、毛髪の太さが40ミクロン(1ミクロン=1/1000ミリ)の場合に毛髪本数(平方ミリメートルあたり本数)が増えると、髪の毛の透け具合がどうなるか(1=完全に透けて見える、つまり完璧なハゲ、0=全然透けて見えない、つまり髪の毛が濃く見える)を示したもので、右下グラフは毛髪の太さが2倍の80ミクロンの場合です。


このグラフを眺めると、まず「毛髪本数が2倍になっても、透け具合(薄毛の見え方)が1/2に手改善するわけではない」ということがわかります。毛髪の本数が増えていくと(グラフの横軸で右側に行くと)、透け具合(縦軸の値)はあまり変わらない(改善しない)ということがわかると思います。
その一方、毛髪の太さが2倍になると、同じ程度の毛髪本数でも、たとえば1平方ミリメートルあたり2〜6本あたり生えている場合を眺めてみれば、毛髪の太さが40ミクロンから80ミクロンになると、髪の毛の透け具合が2倍以上大きく低減することが見て取れます。つまり、薄毛に悩み始めたあたりの人には、毛髪の本数倍増より毛髪の太さ倍増の方が、薄毛(頭部の地肌が透けて見えてしまうこと)を効果的改善するのです*。

ちなみに、薄毛には毛髪本数倍増より太さ倍増が効果的ですが、ハゲ、つまり非常に髪の毛が非常に薄い場合には、本数を増やすことも(毛髪の太さに劣らず)効果的です。上のグラフでも、毛髪本数が非常に少ないあたりでは、毛髪が増えると透け具合が急峻に改善されていることがわかります。だから、あなたの前に「薄毛(ハゲ)の神様」が現れた時、あなたがかなりハゲてるなら「どっちでもOKです!」と叫べばいいし、あなたが薄毛程度なら「毛髪の太さを倍にして下さい!」と答えれば良いのです。
—————————————
*この関係は、実はとても当たり前の関係です。この「薄毛(ハゲ)問題」を考えてみると、「クーポンコレクター問題」の亜種であることがわかります。つまり、大雑把に言えば、「ある程度ランダムに髪の毛が生えているとき、地肌を(重ならず)覆い尽くす組み合わせを得る(コンプリートする)には、毛髪は何本必要か」というのが、この薄毛(ハゲ)問題の本質です。
この毛髪コンプリート問題を考えてみれば、毛髪太さが太いとコンプリートする難易度が低く・少ない毛髪本数でよいのですが、毛髪太さが細いと、コンプリートする難易度が上がり、毛髪をたくさん増やしていっても…なかなかコンプリートしない(=地肌が透けて見える箇所がある)というようになるのです。
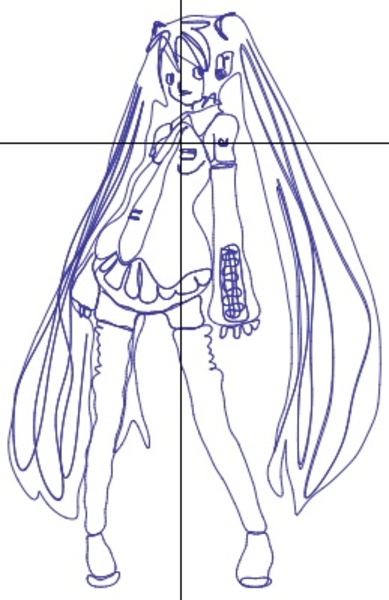
「フィールズ賞はもらった!:初音ミクの数式が解明 さらにいろんな「俺の嫁」が関数で描けることが判明」という記事を読みました。記事内容は、(数式処理ソフトMathematicaの開発元である)Wolfram researchが提供している知識検索エンジンWonfram Alphaが、信じられない図柄、たとえば初音ミクの姿や(Dr.スランプの)アラレちゃんなどの図柄を描き出す「曲線数式」を、次々と作り出すことができる、というものです。
実は、こうした曲線数式は、「フーリエ記述子」という技法を使って自動・単純作業から簡単に作り出すことができるものです。ちなみに、「フーリエ記述子」というのは、たとえば次のようなテクニックです。
まず、数式に変換したい図柄を「(その図柄を描く)曲線の集まり」として分解します。たとえば、もしも図柄が(曲線の集合として表現される)ベクター・グラフィックスでしたら、そのファイルを読み込むだけで、「(その図柄を描く)曲線の集まり」になりますし、あるいは濃淡の画像であれば、たとえば、濃淡の度合いに応じた等高線を描き、その等高線を曲線として考えれば、「(その図柄を描く)曲線の集まり」とすることができます。
次に、それらの曲線(群)を「パラメータで表される曲線」と考えます。たとえば、曲線を各部分での方向(角度)変化という「パラメータの列(集まり)」で表すこともできます。…たとえば、そんな風に、曲線を「パラメータ列」で表現される曲線だと考えてみるのです。
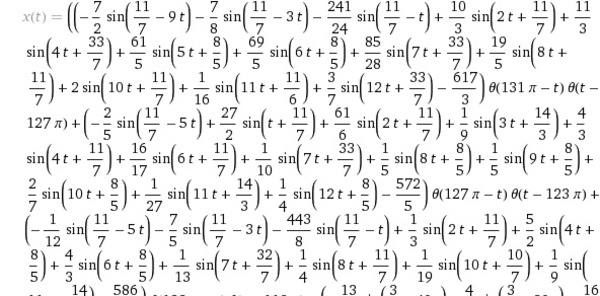
すると、そんなパラメータ列をフーリエ変換することができます。つまり、高校か大学教養あたりで学ぶ、「任意の周期関数は、三角関数を足し合わせとして表現できる」というフーリエ変換を使えば、ありとあらゆる(任意の図柄を表現する)曲線を描くパラメータ列を三角関数の足し合わせ(フーリエ級数)として表すことができます。…これが、図形のフーリエ記述子による表現テクニックです。
最後に、フーリエ変換によりさまざまな三角関数の足し合わせにより表現された(図柄を描く)曲線群を、低次の三角関数だけで表してしまえば(高次の三角関数を省略すれば)、高周波数成分が消えることで滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になります(数式も当然短くなります)。あるいは、高次の項(高周波数の三角関数)まで使えば、微細な模様までも描き出すリアルな曲線を得ることもできます。こういった作業は、単純な数値演算により自動で行うことができます。

…実際、Wolfram Alpha上で「(さまざまな図柄を表示するための)曲線の数式」を眺めてみれば、それらはすべて「三角関数の足し合わせ」で表されていることがわかります(つまり、数学的には、実際のところ、それほど美しいものではありません)。これらが、知識検索エンジンWolfram Alphaが作り出す「さまざまな曲線数式」の作りテクニックの秘密です。

——————————–
関連記事:■Wolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピ
「フーリエ記述子で表現された数式」は美しい存在ではありませんが、(多種多様な存在を単純で良い性質を持つ三角関数の集まりへと分解する)フーリエ級数は実に単純かつ美しい(そして現在のテクノロジーをありとあらゆる分野で支えている何より便利な)存在です。…もしも、教科書の中、目次や頁の先に、「フーリエ級数」なんて項目を見つけたら、その美しさと便利さに感動すること間違いありません。
■上手(かみて)が日本では「自分の左手」になり、西洋では「自分の右手」になった理由

日本では「(自分の)左側」が、「優位な側」である上手(かみて)です(参考:ひな人形の「男雛と女雛が逆になる」までの詳しい歴史)。
もちろん、その逆方向である自分の右側は、「位が下」となる下手(しもて)です。
それを「眺める側」からの向きで言い換えると、向かって右側が上手で、向かって左側が下手、ということになります。
(自分の)左側が「優位」と捉えられるようになった理由には諸説ありますが、よく言われる理由が「南面した時、太陽が上り来る方向=東が、左側になるから」という理由です。
日本とは逆に、ヨーロッパ・中東などの国では、(自分の)左側ではなく右側が「優位な側」とされます。
なぜそうなったかには…これも諸説ありますが、右利きの人が多いので「右側が強い側(左側は弱い側)」とされたとか、「太陽がのぼり来る東を向いた時、太陽が日中指す方向=南が(自分の)右側になるから」という理由が挙げられます。
日本でも西洋でも、優位・尊ばれる側が「太陽が昇る東」や「日中に太陽が位置する南」に由来した、つまり「太陽」を崇拝する心に由来して「有意な側」を決められたという由来は、とても興味深いところです。そしてまた、同じ太陽崇拝に由来したのに、東を向くか(そして南を指すか)・南を向くか(そして東を指すか)という違いが上手(かみて)となる側を左右逆転させたというのも、非常に面白いのではないでしょうか。
■「右の頬を打たれたら、左の頬を…」に隠された意外な秘密

「右」や「左」と言えば、「右の頬を打たれたら左の頬をも向けなさい “But whoever strikes you on your right cheek, turn to him the other also.”」という言葉があります。新約聖書マタイ福音書5:38-42 の中に書かれているイエス・キリストの言葉です。
「右と左が、歴史の中でどのように捉えられてきたか」を考えると、この言葉は実はとても奥深い言葉です。
古代ユダヤ世界では、ヨーロッパ・中東諸国では今でも一般的なように、左手は「悪い側」とされていました。そして「悪い左手」は、自分の主張などを行う際には使うことができませんでした。そして、自分より「階級・地位」が下である者に対して、相手を侮辱・叱責する時には、「右手の(手のひら側でなく)甲で相手の頬を打つ」というやり方がされました。
右手の甲で人の頬を打とうとしたら、やってみればわかりますが、相手の右頬を打つことになります。つまり、あなたが「右の頬を打たれた」という状況は、相手が「あなたの階級・地位が下であると捉えつつ、あなたを貶め・侮辱した」ということを意味するわけです。それが、「右の頬を打たれたら、左の頬をも向けなさい」が指す前半部分の状況です。

それでは後半の「左の頬をも向けなさい」は、一体どういう意味・状態になるのでしょうか。あなたの右頬を打った相手に、あなたが「左の頬を向けた」ら、一体どうすることができるでしょう? 相手があなたの頬を打とうとしても、相手は(悪い側の)左手は使えませんから、右手であなたの左頬を打つことになります。もちろん、あなたの左頬を右手で打とうとすると、相手は右手の甲ではなく、手のひらで打つことになります。
しかし、(自分より相手が下だとみなす行為である)手の甲で打つのではなく、「手のひらで相手を打つ」ということは、相手にとって「自分とあなた」を対等だとみなすことです。つまり、「自分より身分が下」だと蔑んでいる相手を、「自分と同等の人間である」と認める行為となってしまうわけです。
つまり、「右の頬を打たれたら左の頬をも向けなさい」という言葉は、「相手の暴力・差別に対して服従・無抵抗になれ」という意味では決してなく、「相手と自分は対等・平等だという態度・意志を示せ」という言葉だった、というわけです。
この言葉、新約聖書マタイ福音書に書かれている「右の頬を打たれたら・・・」は、旧約聖書の「目には目を、歯には歯を。手には手を、火傷には火傷を、打ち傷には打ち傷を」 という言葉と対比されることが多いため、「無抵抗主義を示す言葉」に思われがちです。しかし、「右と左の歴史」を遡り眺めてみると、無抵抗どころか根本の意味での大きな抵抗を示せという言葉だったのです。
■当たり前のことや見過ごしがちなことも、理由や意味を深掘りすると、新鮮で意外で面白い!
あたりまえのような言葉や作法も、それらが生まれた理由や経緯を知ると、そして、それらの意味を深掘りしてみると、とても面白く・興味深い内容だったりします。今回は、「左右の順位にまつわる歴史的理由」を振り返り、「右の頬を打たれたら左の…の本当の意味」を考えてみました。