
フェルメールは、普通の風景を柔らかく写実的に描いた17世紀オランダの画家です。そのフェルメールが描いた「ミルクを注ぐ女」の世界を3次元空間として復元したのが、View Paint(Point)です(詳しい動画解説)。「ミルクを注ぐ女」が一点透視図法で精密に描かれていることを利用して、幾何学的な関係式やさまざまな歴史資料を元にして、絵画「ミルクを注ぐ女」が描かれた部屋や登場する人や物を、すべて3次元空間上で作り直した…というわけです。その製作秘話(凸版印刷 奥窪氏)を聞き、一番面白かったのが、「ミルクを注ぐ女」を3D化した際に気づかされたという、「絵画に描かれている、現実の世界ではありえないこと」でした。そのひとつが、「ミルクを注ぐ女」が持つ水差しは「ミルクが流れ出ることは不可能な角度だ」ということです。

確かに「ミルクを注ぐ女」を眺めてみると、「ミルクを注ぐ女」が手に持つ水差しからはミルクが流れ出ることは不可能であることに気づかされます。水差しから滴るミルクは、太さがほぼ一定でおおよそ真っ直ぐ鉛直になっていますから、ほとんど動かない(定常)状態の水差しからミルクが落ちているように見えます。その一方で、画を描く視点は、水差しの口より高い位置にあるにも関わらず、水差しの中(入口の奥)には(地球の重力に従って、水差しの口と同じ高さで・ほぼ水平面になっていなければならないはずの)ミルクが全く描かれていないのです。…つまりは、「ミルクを注ぐ女」が手にする水差しの中には、「流れ出す」ことができるミルクは存在していない、というわけです。一体、これはどういうことなのでしょう? フェルメールは、なぜありえない風景を描いたのでしょうか。
…画を描く時の風景を考えてみると、フェルメール「ミルクを注ぐ女」に描かれていたのは、実は「空の水差しを押さえつける女」だったのではないでしょうか。つまり、モデルの女性に「ミルクが入った水差し」を長時間にわたって手に持ち続けてもらうのは大変ですし、その水差しから延々とミルクを注ぎ続けるのも(水差しの中のミルク量は有限ですから)不可能です。…となると、画を描いた時には、モデルには空の水差しを持たせていたのではないだろうか?と思えてきます。さらには、「水差し」だって決して軽いものではないでしょうから、実は「水差し」の腹部分は陶製容器上に乗せられていて、そんな陶製容器の上に乗っかった「水差し」をモデル女性はただ押さえつけているのではないだろうか?という気がしてきます。そう考えながら「水差し」周りを眺めてみると、水差しは陶器容器に接触している位置関係に見え、水差しを手にする女性の右手は(水差しが陶器容器と接触する点のピッタリ反対側から)陶器容器側に押さえつけてるようにも見えてきます。

さらには、「ミルクを注ぐ女」は空の水差しを陶器容器に乗っけていただけではなく、陶器容器の背後には水差しを乗せるための、つまり女性の左手が水差しの底を持ち上げるための苦労をしなくてすむようにするための、「台」なんかもあったりしたのじゃないだろうか?といった想像すらしたくなります。画を描くフェルメールの前にいたのは、何も入っていない水差しを・陶器容器や(陶器容器の背後に隠された)支持台の上で軽く押さえている女性で、流れ出るミルクは一番最後に「(全く別の瞬間を)重ね書き」されたものだったりするのかもしれない…という想像をしたくなります。
ちなみに、「ミルクを注ぐ女」を3D化した際に気づかされた他のことは、女性の左腕が「ありえないほど太く描かれていた」ということだったそうです。この絵の中心で力強さや存在感を与えている「女性の腕」が、現実とは異なるけれど、フェルメールが描いたものだったのです。

「潮の満ち引き」などを起こす潮汐力に関して「よくある疑問」が、「月に引かれてる」のに「反対側も盛り上がる」のはなんで?という疑問です。
月に引かれて、月に面した側の(海面や地面)が盛り上がろうとするのは納得できるけど、逆側も盛り上がるのは何だかよくわからない…という話をよく聞きます。そこで、今回は、「月に引かれてる」のに「反対側も盛り上がる」理由を図示してみることにします。
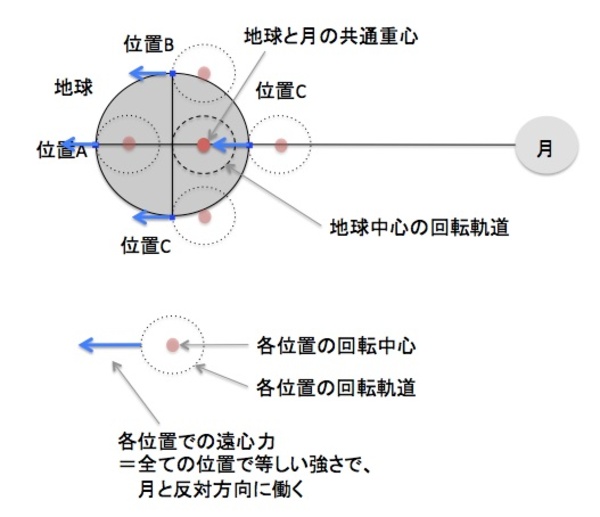
月による潮汐力を考えるため、まず地球と月が引き合いながら回転しているようすを描いてみました。それが、右の図です。地球と月は、(地球と月を合わせた)共通重心を中心として回転(公転)しています。そんな公転を地球上の各位置が行う時には、地表上の各点は同じ等速の円運動を行い、(その等速円運動する状態を基準とすると)どの点も「月がいる方向とは反対側に働く」同じ大きさの遠心力を受けることになります。そして、地球重心では、その遠心力は月の引力と等しい、ということになります。
さて、月と引き合いながら互いに周り合う地球上に働く力を描いてみたのが下の図です。(地面や海面を持ち上げようとする)鉛直方向の力を考えてみると、地表に働く力は「地球の重力」「遠心力」「月の引力」です。「地球の重力」「遠心力」は(実際には重力は場所毎に微妙に違いますが)どこでも同じで、「月の引力」は月との距離にしたがって異なり、月に近い側は強く・月に遠い側は弱い…ということになります。そして、月との公転による遠心力が地球中心での月の引力に等しいということも踏まえて「地球上の各位置での(地球中心に向かって働く)鉛直方向の力」を計算してみると(下図参照)、月の方を向いた側と月の反対側は「地球の重力から(地球中心と表面での)月の引力の差分を引いただけ弱い」ということになり、月を横に見るあたりでは、鉛直方向に働く引力は地球の重力と同じ、ということになります。つまりのところ、月の方を向いた側と月と反対側が、それ以外の場所より「鉛直方向下向きに働く力が弱い」ということになるわけです。どれだけ弱いかというと、「(地球中心と表面での)月の引力の差分だけ」になります。
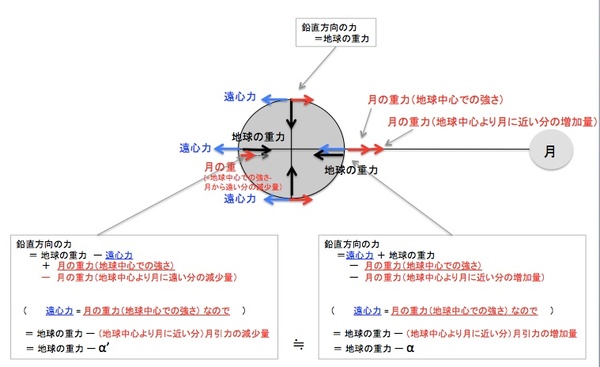
そういうわけで、「月に引かれてる」のに「反対側も盛り上がる」わけです。…あるいは、こんな図を描かなくとも、「月に近い場所ほど強く引っ張られるのだから、月に向かう方向に伸び~るのが当たり前だよね」とも思えるかもしれませんね。
スカートを履いた女性がチョコレートを取ろうとして屈んだ瞬間に、スカートがめくれ上がってしまう、という動画があります。こんな動画を眺めると、どうすれば同じようなテクニックを駆使することができるのか!…じゃなかった、どういう屈み方をすればスカートがめくれ上がらずに済むかを、調べ解き明かしたくなります。そこで、「風でめくれるスカート」の科学!「涼しく晴れた朝の地下鉄駅をドジっ娘が走る」とスカートは必ずめくれる!?の法則の時と同じように、流体力学や衣服学を駆使して「スカートめくれ」を実現する…じゃなかった防ぐための屈み方を考えてみることにしましょう。
まずは、女性が屈み込んでいく際の動きを思い浮かべてみると、およそ2m/s^2くらいの加速度であるように思えます。2m/s^2 程度の加速度で0.5秒くらい下向きに加速して・そして残り0.5秒ほどで屈む速度が減っていき、結果として1秒ほどで50cmくらい屈み込むという具合です。このような動きをすると、腰の部分が下に向かう速度は最大で秒速約1mになります。
次に、腰が秒速約1mで下に屈もうとする時のスカートの動きを考えてみると、スカートに働く力は重力と(下に下がっていくスカートが)スカート上下の空気から受ける抵抗です。それらふたつの力がスカートにかかっている時、一体スカートがどういった動きをするかということを、
- ・スカート端の直径が70cm
- ・スカートの重さが150グラム
という条件で計算してみると、スカートは1.1m/s^2の加速度で下へと動いていく…という結果になります。

女性の腰が2m/s^2 程度の加速度で動いていくのに対して、(それより遅れて)スカートが1.1m/s^2の加速度で下へ動いていく、ということは、女性の腰を基準にすれば、スカートが相対的に2 – 1.1 =0.8m/s^2の加速度で めくれ上がっていく…ということになります。だから、上の動画のように、スッと屈み込もうとした女性のスカートがフワリと浮かび上がってしまったわけです。
それでは、一体どうすれば「スカートがめくれ上がらずに済むか」というと、ほんの少しだけ屈む速度を遅くしてやれば良いのです。たとえば、上のスカート端や重さの条件れあれば、屈み込む加速度を1.8m/s^2よりゆっくりにしてやれば、スカートがめくれ上がることを防ぐことができます。
…というわけで、「スカートめくれ」を防ぐためには、いくら美味しそうなチョコレートが落ちていたとしても、(自分のスカートの大きさや重量から計算して導かれる)一定以下の速度に保つようにするということになります。あるいは、「スカートめくれ」を実現させるためには、思わず屈み込む速度が(計算から導かれた)所定の値を上回るような魅力的な食べ物を落としておく!ということになるのです。
森羅万象・古今東西のスカートのめくれを解き明かすことができるなんて考えると、色んな科学を勉強したくなりますよね!








