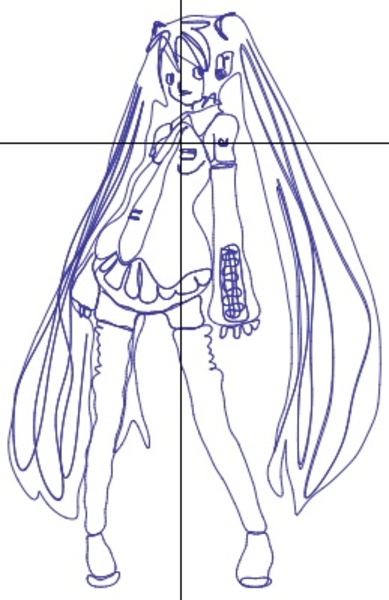
 「フィールズ賞はもらった!:初音ミクの数式が解明 さらにいろんな「俺の嫁」が関数で描けることが判明」という記事を読みました。記事内容は、(数式処理ソフトMathematicaの開発元である)Wolfram researchが提供している知識検索エンジンWonfram Alphaが、信じられない図柄、たとえば初音ミクの姿や(Dr.スランプの)アラレちゃんなどの図柄を描き出す「曲線数式」を、次々と作り出すことができる、というものです。
「フィールズ賞はもらった!:初音ミクの数式が解明 さらにいろんな「俺の嫁」が関数で描けることが判明」という記事を読みました。記事内容は、(数式処理ソフトMathematicaの開発元である)Wolfram researchが提供している知識検索エンジンWonfram Alphaが、信じられない図柄、たとえば初音ミクの姿や(Dr.スランプの)アラレちゃんなどの図柄を描き出す「曲線数式」を、次々と作り出すことができる、というものです。
実は、こうした曲線数式は、「フーリエ記述子」という技法を使って自動・単純作業から簡単に作り出すことができるものです。ちなみに、「フーリエ記述子」というのは、たとえば次のようなテクニックです。
まず、数式に変換したい図柄を「(その図柄を描く)曲線の集まり」として分解します。たとえば、もしも図柄が(曲線の集合として表現される)ベクター・グラフィックスでしたら、そのファイルを読み込むだけで、「(その図柄を描く)曲線の集まり」になりますし、あるいは濃淡の画像であれば、たとえば、濃淡の度合いに応じた等高線を描き、その等高線を曲線として考えれば、「(その図柄を描く)曲線の集まり」とすることができます。
次に、それらの曲線(群)を「パラメータで表される曲線」と考えます。たとえば、曲線を各部分での方向(角度)変化という「パラメータの列(集まり)」で表すこともできます。…たとえば、そんな風に、曲線を「パラメータ列」で表現される曲線だと考えてみるのです。
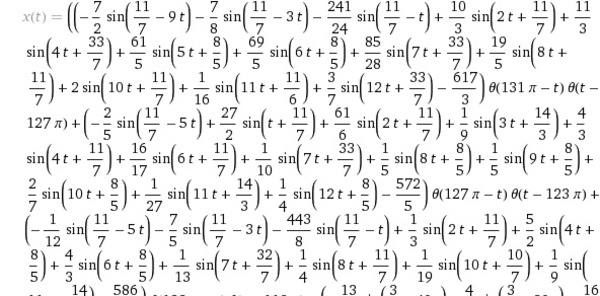 すると、そんなパラメータ列をフーリエ変換することができます。つまり、高校か大学教養あたりで学ぶ、「任意の周期関数は、三角関数を足し合わせとして表現できる」というフーリエ変換を使えば、ありとあらゆる(任意の図柄を表現する)曲線を描くパラメータ列を三角関数の足し合わせ(フーリエ級数)として表すことができます。…これが、図形のフーリエ記述子による表現テクニックです。
すると、そんなパラメータ列をフーリエ変換することができます。つまり、高校か大学教養あたりで学ぶ、「任意の周期関数は、三角関数を足し合わせとして表現できる」というフーリエ変換を使えば、ありとあらゆる(任意の図柄を表現する)曲線を描くパラメータ列を三角関数の足し合わせ(フーリエ級数)として表すことができます。…これが、図形のフーリエ記述子による表現テクニックです。
最後に、フーリエ変換によりさまざまな三角関数の足し合わせにより表現された(図柄を描く)曲線群を、低次の三角関数だけで表してしまえば(高次の三角関数を省略すれば)、高周波数成分が消えることで滑らかで丸っこい曲線になります。つまり、手書きした感じの図形になります(数式も当然短くなります)。あるいは、高次の項(高周波数の三角関数)まで使えば、微細な模様までも描き出すリアルな曲線を得ることもできます。こういった作業は、単純な数値演算により自動で行うことができます。

…実際、Wolfram Alpha上で「(さまざまな図柄を表示するための)曲線の数式」を眺めてみれば、それらはすべて「三角関数の足し合わせ」で表されていることがわかります(つまり、数学的には、実際のところ、それほど美しいものではありません)。これらが、知識検索エンジンWolfram Alphaが作り出す「さまざまな曲線数式」の作りテクニックの秘密です。
 ——————————–
——————————–
関連記事:■Wolfram Alphaが「色んな形を描き出す曲線を作る」ためのレシピ
「フーリエ記述子で表現された数式」は美しい存在ではありませんが、(多種多様な存在を単純で良い性質を持つ三角関数の集まりへと分解する)フーリエ級数は実に単純かつ美しい(そして現在のテクノロジーをありとあらゆる分野で支えている何より便利な)存在です。…もしも、教科書の中、目次や頁の先に、「フーリエ級数」なんて項目を見つけたら、その美しさと便利さに感動すること間違いありません。
宮澤賢治「銀河鉄道の夜」は、「少年ジョバンニ*が、灯籠流しが行われた夜に丘の上から銀河鉄道に乗り、級友カムパネルラと天空の旅をする。丘の上でジョバンニがひとり気づくと、カムパネルラは川で人を助けた後に行方不明になったということを知る」という話です。
 主人公の級友であり、(亡くなった時に)主人公と銀河鉄道を共に旅をしたカムパネルラの名前は、イタリア・ルネッサンス時代の哲学者「トンマーゾ・カンパネッラ** Tommaso Campanella」からとられている、と言われています。宮澤賢治が盛岡中学(現・盛岡第一高等学校)と盛岡高等農林学校(現・岩手大学農学部)に在学していた頃、大西 祝 著「西洋哲学史」(初版は明治36年)を読み、そこに書かれていた「カンパネッラ」に強く惹かれ、銀河鉄道の夜の「主人公と別れ・亡くなった級友」の名前をカムパネルラとした、というのです。当時の他書物では(それ以降も)、トマソ・カンパネッラの名前がカンパネラ(カンパネッラ)と書かれているのに対して、大西 祝 著「西洋哲学史」の記述のみが(宮澤賢治が銀河鉄道の夜で書いたのと同じ)カムパネルラと書かれている、というのがその傍証のひとつです。
主人公の級友であり、(亡くなった時に)主人公と銀河鉄道を共に旅をしたカムパネルラの名前は、イタリア・ルネッサンス時代の哲学者「トンマーゾ・カンパネッラ** Tommaso Campanella」からとられている、と言われています。宮澤賢治が盛岡中学(現・盛岡第一高等学校)と盛岡高等農林学校(現・岩手大学農学部)に在学していた頃、大西 祝 著「西洋哲学史」(初版は明治36年)を読み、そこに書かれていた「カンパネッラ」に強く惹かれ、銀河鉄道の夜の「主人公と別れ・亡くなった級友」の名前をカムパネルラとした、というのです。当時の他書物では(それ以降も)、トマソ・カンパネッラの名前がカンパネラ(カンパネッラ)と書かれているのに対して、大西 祝 著「西洋哲学史」の記述のみが(宮澤賢治が銀河鉄道の夜で書いたのと同じ)カムパネルラと書かれている、というのがその傍証のひとつです。
実は、カムパネルラ(トンマーゾ・カンパネッラ)の名前は、ジョバン・ドメーニコ・カンパネッラ Giovan Domenico Campanella でした。トンマーゾというのは、後に修道士になった時に付けた聖職者名です。つまり、カムパネルラの名前はジョバン(ニ)で、ジョバンニは、カムパネルラでもあったのです。
 問題は、カムパネルラの名前がジョバン(ニ)でもあったことを、それを果たして「銀河鉄道の夜」という物語を書き綴った作者、宮澤賢治自身が知っていたかどうか?です。宮澤賢治が読んでいたとされる大西 祝 著「西洋哲学史」に、カムパネルラの幼名が書かれていたなら単純明快、「知っていた」で決まりです。…しかし、話はそう単純ではありません。なぜかというと、大西 祝 著「西洋哲学史」のカムパネルラに関する記述には、ジョバンといった幼名は一切書かれていないからです。
問題は、カムパネルラの名前がジョバン(ニ)でもあったことを、それを果たして「銀河鉄道の夜」という物語を書き綴った作者、宮澤賢治自身が知っていたかどうか?です。宮澤賢治が読んでいたとされる大西 祝 著「西洋哲学史」に、カムパネルラの幼名が書かれていたなら単純明快、「知っていた」で決まりです。…しかし、話はそう単純ではありません。なぜかというと、大西 祝 著「西洋哲学史」のカムパネルラに関する記述には、ジョバンといった幼名は一切書かれていないからです。
右に貼り付けた画像は、大西 祝 著「西洋哲学史」でカムパネルラが解説されている頁です(左上に太字でカムパネルラと書いてあるのがわかるでしょう)。実際に確認してみても、幼名はおろか、トンマーゾという名すら書かれていません(もちろん、この次頁にも書かれていません)。「西洋哲学史」にカムパネルラについては2頁にわたり書かれていても、そのカムパネルラの名前がジョバン(ニ)でもあったことは触れられていないのです。
 宮澤賢治が他書籍からカムパネルラの幼名を知ったという可能性もゼロではありませんが、そうだったとすれば、(他書籍で使われる)カンパネラでなく(西洋哲学史でのみ使われる)カムパネルラと書いている理由が説明されなくなってしまうのです。すると、宮澤賢治はカムパネルラ=ジョバン(ニ)だったということを知らずに、何かの偶然で、この名前の組み合わせを使ったということなのでしょうか?
宮澤賢治が他書籍からカムパネルラの幼名を知ったという可能性もゼロではありませんが、そうだったとすれば、(他書籍で使われる)カンパネラでなく(西洋哲学史でのみ使われる)カムパネルラと書いている理由が説明されなくなってしまうのです。すると、宮澤賢治はカムパネルラ=ジョバン(ニ)だったということを知らずに、何かの偶然で、この名前の組み合わせを使ったということなのでしょうか?
けれど、それも「できすぎた話」のようにも思えます。同じ列車に乗り合わせた(まるで自分の片割れのような)存在と別れていくという「銀河鉄道の夜」の物語中で、それらふたつでひとつ存在に、カムパネルラとジョバン(ニ)という「ひとり」の名前が付けられているなんて、何だか偶然だとは思い難い話です。ジョバンがヨハンに由来するとてもポピュラーな名前だとは言え、「偶然の一致」とするには少しばかり無理があります。…というわけで、「銀河鉄道の夜」カムパネルラ=ジョバンニだったと宮澤賢治は果たして知っていたかどうか、それが「とても興味深い、物語作りにまつわるミステリー」なのです。
 ちなみに、カムパネルラという名は、イタリア語の「(教会の)小さな鐘を鳴らす」という仕事に由来するファミリー(姓)名です。こんな由来は、さすがに宮澤賢治が知ることはなかったことでしょうが、水面へと、空へと、亡くなった人を悼む灯籠がゆらり流されていく「銀河鉄道の夜」にすごく似合う名前だとは思いませんか。
ちなみに、カムパネルラという名は、イタリア語の「(教会の)小さな鐘を鳴らす」という仕事に由来するファミリー(姓)名です。こんな由来は、さすがに宮澤賢治が知ることはなかったことでしょうが、水面へと、空へと、亡くなった人を悼む灯籠がゆらり流されていく「銀河鉄道の夜」にすごく似合う名前だとは思いませんか。
カムパネルラ、…どこまでも どこまでも 一緒に行こう
「銀河鉄道の夜」
————
*ジョバンニという名前は、宮澤賢治の「ひのきとひなげし」にも「セントジョバンニ」として登場しています。
**カンパネッラは強い信仰と自然に学ぶ科学を指向する矛盾を抱え、宮澤賢治自身を彷彿させます。ちなみに、カンパネッラは71年の人生中の32年を監禁・幽閉で過ごしました。その中のいくばくかは、第2次ガリレオ裁判でガリレオの弁護をしたため、という人です。
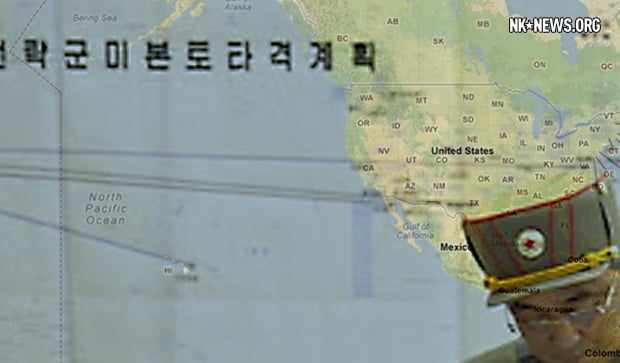 「北朝鮮の金正恩第1書記が3月29日、軍の作戦会議を緊急招集し”アメリカ本土へのミサイル攻撃計画”に署名した」北朝鮮メディアが伝えました。しかし、その北朝鮮国内報道で流れた「作戦会議の写真」には、アメリカ本土攻撃計画が見事に映り込んでいて、ミサイルをアメリカのどこに向けようとしているかが、丸わかりだった、という解析がされています(他には金正恩第1書記が21.5インチのApple iMacを使っているとか)。
「北朝鮮の金正恩第1書記が3月29日、軍の作戦会議を緊急招集し”アメリカ本土へのミサイル攻撃計画”に署名した」北朝鮮メディアが伝えました。しかし、その北朝鮮国内報道で流れた「作戦会議の写真」には、アメリカ本土攻撃計画が見事に映り込んでいて、ミサイルをアメリカのどこに向けようとしているかが、丸わかりだった、という解析がされています(他には金正恩第1書記が21.5インチのApple iMacを使っているとか)。
 日本国内に住んでいる私たちからすると、北朝鮮ミサイルが狙う「アメリカ本土ターゲット」も気になりますが、それより何より、日本国内のターゲットが一番知りたいところです。そこで、(右に貼り付けた)北朝鮮の緊急作戦会議の写真をじっくり調査してみると、金正恩第1書記が座り・作業するピカピカ机の表面、金正恩第1書記の右手の先辺りに、日本周辺地図がわずかに映り込んでいます。そこで、その映り込みに画像処理を掛けて、拡大・復元してみた結果が下の写真です。見事に、北朝鮮作戦会議で映し出されている日本周辺地図が浮かび上がっています。
日本国内に住んでいる私たちからすると、北朝鮮ミサイルが狙う「アメリカ本土ターゲット」も気になりますが、それより何より、日本国内のターゲットが一番知りたいところです。そこで、(右に貼り付けた)北朝鮮の緊急作戦会議の写真をじっくり調査してみると、金正恩第1書記が座り・作業するピカピカ机の表面、金正恩第1書記の右手の先辺りに、日本周辺地図がわずかに映り込んでいます。そこで、その映り込みに画像処理を掛けて、拡大・復元してみた結果が下の写真です。見事に、北朝鮮作戦会議で映し出されている日本周辺地図が浮かび上がっています。

 日本の上には何カ所か情報が書かれていて、そのうち2箇所に明瞭なマークが描かれています。2箇所のマークのうち、おそらく、一箇所は自衛隊の呉基地で、もう一箇所は厚木基地のように見えます。その他の、情報が書かれている場所は八戸基地や大湊基地辺りでしょうか。…とにかく、北朝鮮の作戦会議に写るモニタ画面上では、日本国内の重要ターゲットは厚木基地と呉基地のようです*。北朝鮮がミサイルを撃ちそうな時が来たら、厚木と呉近くには立ち入らない方が良いのかもしれません。
日本の上には何カ所か情報が書かれていて、そのうち2箇所に明瞭なマークが描かれています。2箇所のマークのうち、おそらく、一箇所は自衛隊の呉基地で、もう一箇所は厚木基地のように見えます。その他の、情報が書かれている場所は八戸基地や大湊基地辺りでしょうか。…とにかく、北朝鮮の作戦会議に写るモニタ画面上では、日本国内の重要ターゲットは厚木基地と呉基地のようです*。北朝鮮がミサイルを撃ちそうな時が来たら、厚木と呉近くには立ち入らない方が良いのかもしれません。
ところで、この北朝鮮の作戦会議に貼られた太平洋周辺地図(から復元した日本周辺地図)を眺めていると、「成田空港のあたりから、何本も線が世界へと延びている」ように見えるのは…きっと気のせいですよね。
—————–
*呉ではなくて神戸なのではないか説も濃厚です。
 「フィールズ賞はもらった!:初音ミクの数式が解明 さらにいろんな「俺の嫁」が関数で描けることが判明」という記事を読みました。記事内容は、(数式処理ソフトMathematicaの開発元である)Wolfram researchが提供している知識検索エンジンWonfram Alphaが、信じられない図柄、たとえば初音ミクの姿や(Dr.スランプの)アラレちゃんなどの図柄を描き出す「曲線数式」を、次々と作り出すことができる、というものです。
「フィールズ賞はもらった!:初音ミクの数式が解明 さらにいろんな「俺の嫁」が関数で描けることが判明」という記事を読みました。記事内容は、(数式処理ソフトMathematicaの開発元である)Wolfram researchが提供している知識検索エンジンWonfram Alphaが、信じられない図柄、たとえば初音ミクの姿や(Dr.スランプの)アラレちゃんなどの図柄を描き出す「曲線数式」を、次々と作り出すことができる、というものです。
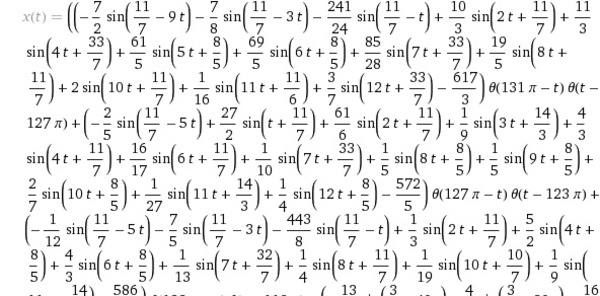 すると、そんなパラメータ列をフーリエ変換することができます。つまり、高校か大学教養あたりで学ぶ、「任意の周期関数は、三角関数を足し合わせとして表現できる」というフーリエ変換を使えば、ありとあらゆる(任意の図柄を表現する)曲線を描くパラメータ列を三角関数の足し合わせ(フーリエ級数)として表すことができます。…これが、図形のフーリエ記述子による表現テクニックです。
すると、そんなパラメータ列をフーリエ変換することができます。つまり、高校か大学教養あたりで学ぶ、「任意の周期関数は、三角関数を足し合わせとして表現できる」というフーリエ変換を使えば、ありとあらゆる(任意の図柄を表現する)曲線を描くパラメータ列を三角関数の足し合わせ(フーリエ級数)として表すことができます。…これが、図形のフーリエ記述子による表現テクニックです。

 ——————————–
——————————–








