今週末の１１月３日（Sun）と４日（Mon）、東京お台場の科学未来館で開催されるMaker Faire Tokyo 2013に「Twitter連動バブルジェットディスプレイ」を出展します（科学未来館一階，オリエンテーションルーム N-12ブース）。Twitter連動バブルジェットディスプレイというのは、Twitterで（専用アカウント @awatwi 宛に）つぶやくと、そのつぶやきを水の泡で描き出す”バブルジェットディスプレイ”です。コンセプトは、ふとしたときに生まれる「つぶやき」なんて、まるで小さな泡みたいな存在だから、そのつぶやきに似合った表示形態を作ってやろう！というものです。
みずのあわ【水の泡】とは；
① 水の上に浮かぶ泡。
② はかなく消え去るもの。
③ 努力や苦心などがむだになること。
「せっかくの苦労も―だ」
Maker Faire は面白い奇妙な工学技術自作グッズがたくさん並ぶ祭典ですから、モノを作る・作ったものを見るのが好きな人は遊びに行くと面白いかもしれません。開催時間は、3日（日）は12:00～17:00、4日（月）は10:00～17:00です。
3日・4日の両日とも、開催時間中は、ブース辺りで所在なくぼおっと立ってると思いますので、お気軽に声をお掛け下さい。また、ブース辺りに姿が見えなく・近くをウロウロ右往左往しているようでしたら、 @hirax, jun@hirax.netにでも、適当に声をお掛け下さい。
それでは、１１月２・３日はMaker Faire Tokyo 2013でお会いしましょう！
「短いスカートが身体に悪影響を与えることが科学的に証明されました。」というポスターを、学校の構内で見かけました。 ポスターの内容は、「（膝位置より１５ｃｍ短い）短いスカートは体温低下を生じさせ、体温低下は免疫低下や血圧上昇を生じさせる」というものです。このポスター、「短」「悪」という２文字が強調されていて、短いスカートを履いた瞬間、悪の組織から恐怖の毒電波が飛んでくる…ような感覚に陥ります（特に右下のポスターは、悪の組織に誘われ・地球征服の手先にされてしまいそうな雰囲気です）。
スカート丈が短ければ、身体の露出面積は増えますから（「スカート丈の長短が衣服気候へ及ぼす影響について 聖徳栄養短期大学紀要 3, 27-31, 1971-03-20」によれば、身体の被覆率は、（半袖状態の）膝丈スカートで６３％、膝上１０ｃｍスカートで５７％、膝上２０ｃｍで５２％となっています）、気温が低かったり・風を受ける状態では、短いスカートを履くと、身体から多少なりとも熱が奪われてしまうことでしょう。だから、寒い日には短いスカートは身体に優しくない…というのは、とても自然な話です。
しかし、寒い日には短いスカートは（身体が冷えて）身体に悪いということだとすると、「寒くない暑い日であれば、短いスカート丈の方が身体にいい」ということにもなりそうです。
たとえば、「（以前作成した）世界各国で調査された「気温と（その時期の衣服による）肌の被覆率」によると、気温が２５℃なら肌被覆率は６０％くらい、３０℃なら５０％ほどです。つまり、気温が暑くなると、衣服で身体を覆わず・露出するのが普通になります。
このデータをスカートだけに適用してみると、気温２５℃ならスカート丈は膝上５ｃｍくらい、気温３０℃ならスカート丈は膝上２０ｃｍ強くらいでも自然かも…ということになってもおかしくありません。
だから、コンクリートジャングルな日本の大都市で、夏の暑さが厳しくなっていく未来には、「長いスカートは身体に悪影響を与えることが科学的に証明されました」というポスターが学校港内に張られていたりするかもしれません。
——————————-
…それにしても、私が中学の時代には、「長いスカート」が「不良・スケバン」の象徴・悪の象徴とされていました。それとは逆に、今の時代は「短いスカート」が悪とされている…というのは、何だか不思議な心地です。
「何人が集まれば、同じ誕生日の人（たち）がいる確率が50％を超えるか?」という問題があります。
計算すると、その答えは「23人」となり、意外に少ない人数でも「同じ誕生日の人たちがいる確率が高い」ので、誕生日のパラドックスと言われたりします。計算自体は、
同じ誕生日の人たちがいる確率＝1-同じ誕生日の人たちがいない確率
なので、「同じ誕生日の人たちがいない確率」を誕生日が重ならない条件と考えれば、たとえば23人であれば
＝1 – 364/365 × 363/365 × 362/365 …× (365-23 + 1) / 365
＝0.50729723432398540723…
と計算することができて、その確率は５０パーセントを超えるというわけです（詳しくはたとえばこちら）。
ところで、戦前の日本の月別出生率を眺めると、誕生日が１〜３月に集中していたことがわかります。たとえば、「1899年から2000年までの月別出生率」を見ると、「１月・２月・３月の出生率が他の月の1.5倍くらい高く」「一番出生率が少ない６月と比べると、１〜３月は２倍ほど高い」という具合になっています。（データが途切れてる箇所が太平洋戦争時です）
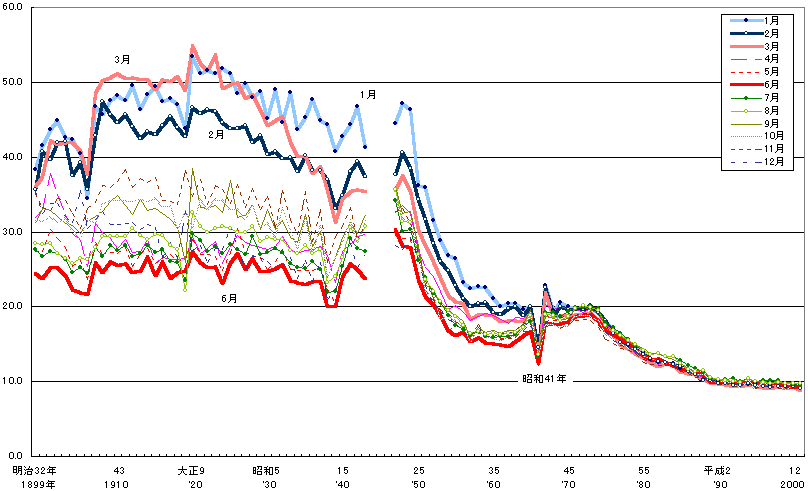
さて問題です。このような誕生日が１〜３月の時期に集中していた戦前の日本で「誕生日のパラドックス」を考えてみると、つまり「何人が集まれば、同じ誕生日の人（たち）がいる確率が50％を超えるか?」を考えてみると、一体どんな答が出てくるでしょう？…真夏の夜に挑戦するのに丁度良い面白いパズルだと思いませんか？直感的には、何人いれば同じ誕生日の人たちがいる確率が５０％を超えると思いますか？
