雑学界の権威・平林純の考える科学

　「潮の満ち引き」などを起こす潮汐力に関して「よくある疑問」が、「月に引かれてる」のに「反対側も盛り上がる」のはなんで？という疑問です。 月に引かれて、月に面した側の（海面や地面）が盛り上がろうとするのは納得できるけど、逆側も盛り上がるのは何だかよくわからない…という話をよく聞きます。そこで、今回は、「月に引かれてる」のに「反対側も盛り上がる」理由を図示してみることにします。

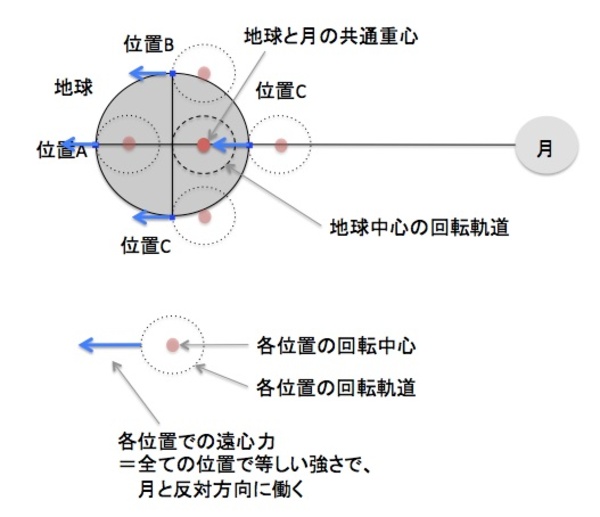
　月による潮汐力を考えるため、まず地球と月が引き合いながら回転しているようすを描いてみました。それが、右の図です。地球と月は、（地球と月を合わせた）共通重心を中心として回転（公転）しています。そんな公転を地球上の各位置が行う時には、地表上の各点は同じ等速の円運動を行い、（その等速円運動する状態を基準とすると）どの点も「月がいる方向とは反対側に働く」同じ大きさの遠心力を受けることになります。そして、地球重心では、その遠心力は月の引力と等しい、ということになります。

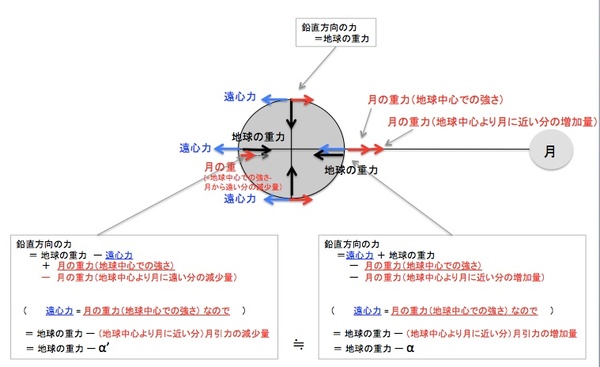
　さて、月と引き合いながら互いに周り合う地球上に働く力を描いてみたのが下の図です。（地面や海面を持ち上げようとする）鉛直方向の力を考えてみると、地表に働く力は「地球の重力」「遠心力」「月の引力」です。「地球の重力」「遠心力」は（実際には重力は場所毎に微妙に違いますが）どこでも同じで、「月の引力」は月との距離にしたがって異なり、月に近い側は強く・月に遠い側は弱い…ということになります。そして、月との公転による遠心力が地球中心での月の引力に等しいということも踏まえて「地球上の各位置での（地球中心に向かって働く）鉛直方向の力」を計算してみると（下図参照）、月の方を向いた側と月の反対側は「地球の重力から（地球中心と表面での）月の引力の差分を引いただけ弱い」ということになり、月を横に見るあたりでは、鉛直方向に働く引力は地球の重力と同じ、ということになります。つまりのところ、月の方を向いた側と月と反対側が、それ以外の場所より「鉛直方向下向きに働く力が弱い」ということになるわけです。どれだけ弱いかというと、「（地球中心と表面での）月の引力の差分だけ」になります。

　そういうわけで、「月に引かれてる」のに「反対側も盛り上がる」わけです。…あるいは、こんな図を描かなくとも、「月に近い場所ほど強く引っ張られるのだから、月に向かう方向に伸び~るのが当たり前だよね」とも思えるかもしれませんね。