こうした現象を理解し、さらに活用するために役立つのが、グレア錯視という視覚・認知の特性を理解しておくことです。グレア錯視というのは、たとえば、暗い背景の中に明るい部分が明るい領域があり、その境界に明るさや色のグラデーションが存在していると、明るい部分をより明るく・眩しく感じる、という特性です。
たとえば、下の画像を眺めてみると、左画像の中央にある白い部が(右のグラデーションがない画像の中央白い部分より)明るく・眩しく感じられるはずです。これが、グレア錯視です。
あるいは、カメラのレンズによるボケなどにより、輝く被写体がグラデーションを帯びつつボケた写りになる状況も多いものです。
そういった時にも、グレア錯視を意識しつつ、さらに被写体を明るく・眩しく感じさせるような仕掛けを入れてみる、ということもできそうです。
八算 」の存在を知らない人も多いかもしれません。
八算は、中国で割り算を計算するために使われていた「九帰」が元になっています。そして、「1で割っても値が変わらない」ことから1の段が省略されて八算と称されるようになりました。そのため、2の段冒頭「二一天作五(にいちてんさくのご)=10を2で割ると五ができる」というように、「割る数・割られる数(*10)・割った結果・(あれば余り)」の順で割り算の結果を並べて、暗記したものです。ちなみに、二一天作五の次は「二進一十(にしんがいんじゅう)=20を2で割ると10になる」「三一三十一(さんいちさんじゅうのいち)=10を3で割ると3余り1になる」というように続いていきます*。
八算は九九と同じくらい一般的でしたし、時には掛け算の九九より好んで使われることも多かったといいます。たとえば、「ねずみが3匹いて、頭数が1日毎に2倍に増えていくとき、n日目には何匹いるか?」を計算するときに、「2倍する」という計算をn回繰り返すのではなく、「10倍して(桁を上げて)5で割る」という計算をn回繰り返すやり方の方が、かつては好まれました。なぜかというと、八算とそろばんを使うと、「5(に限らずある数字)で割り続ける」という作業がとても簡単だったからです。
「九九」より使われていた割り算版「九九」である八算は、昭和初期までは学校で広く教えられていましたし、そろばん計算をする際には、昭和の中頃までも使われていたといいます。けれど、その後掛け算を多く用いるやり方が多く使われるようになり、今では忘れられた存在になってしまいました。忘れられてしまったけれど、実はとても楽に計算をすることができる「八算」、頭のパズルがてら、その存在を振り返ってみるのはいかがでしょうか。
——————
機構的には単純で、ドミノが傾き・倒れていく時のことを考えると、「次のドミノにぶつかる」瞬間には、(理想的な配置にして・空気抵抗やドミノ間の表面摩擦などを無視してやると)約1.7〜8倍程度「自分より大きなドミノ」を倒れ始めさせることができる程度の運動エネルギーを持ちます**。もちろん、そのエネルギーはゼロからいきなり生み出されたわけではなくて、ドミノが立ってた時の位置エネルギーの一部が運動エネルギーと姿を変えたものです。ドミノが倒れると、自分と同じ程度のドミノを倒すだけだけでなく、さらに巨大なドミノを倒すことができる程度のエネルギーが放出されるわけです。
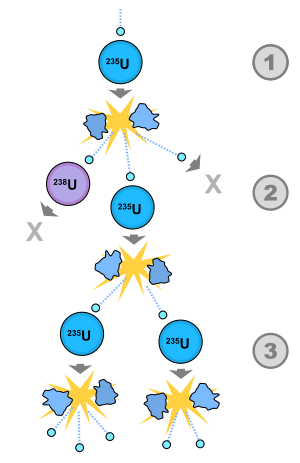
つまり、ドミノを倒れさせるために必要なエネルギーより、ドミノが倒れた時に放出されるエネルギーが大きいので、その「より大きなエネルギーを放出する」割合にしたがって、多くのドミノや、自分より大きいドミノを倒していくことは当然できる…というわけです。それはまさに、「核分裂反応が次々と核分裂反応を引き起こして、指数関数的に核分裂が次々と増加していくさま」を思い起こさせます。そこで、約30年前、「指数関数的に巨大化するドミノ倒し実験のデモンストレーション実験」が核分裂連鎖反応を説明するために考案されたわけです。
核分裂の連鎖反応に限らず、ほんの少しのことをキッカケとして、雪崩のように次々と大きなことことがひき起こされていく…ということはよくあるものです。そういった現象の姿を…手元にある消しゴムや本や雑誌をドミノのように並べ・次々と倒す実験をすることで(お母さんとかに怒られることは覚悟の上で)体感・想像してみると面白いかもしれません!?
ーーーーーーーーーーー
 右の画像は、モネがえがいた「夕日の国会議事堂」です。この絵の夕日部分を眺めると、とても眩しく明るく感じます。
けれど、よくよく考えてみると、少し不思議なことに気がつきます。夕日部分を塗っている色自体は、決して、光り輝くようなとても明るい色というわけではありません。けれど、モネ描く夕日を、私たちはとても眩しく感じているのです。
右の画像は、モネがえがいた「夕日の国会議事堂」です。この絵の夕日部分を眺めると、とても眩しく明るく感じます。
けれど、よくよく考えてみると、少し不思議なことに気がつきます。夕日部分を塗っている色自体は、決して、光り輝くようなとても明るい色というわけではありません。けれど、モネ描く夕日を、私たちはとても眩しく感じているのです。

 だから、右のような夕日の周りに明るさや色のグラデーションがある写真を見ると、夕日部分の輝度は(撮影時に飽和してしまい)「ただの白色」に過ぎないはずなのに、明るく眩しく輝いているように感じられるのです。逆に言えば、明るい部分が飽和してしまいそうな状況でも、明るい部分の周りにグラデーションを写し込んでおけば、後で眺めるときにも「ちゃんと明るく感じる」ことができる、というわけです。
だから、右のような夕日の周りに明るさや色のグラデーションがある写真を見ると、夕日部分の輝度は(撮影時に飽和してしまい)「ただの白色」に過ぎないはずなのに、明るく眩しく輝いているように感じられるのです。逆に言えば、明るい部分が飽和してしまいそうな状況でも、明るい部分の周りにグラデーションを写し込んでおけば、後で眺めるときにも「ちゃんと明るく感じる」ことができる、というわけです。
 そしてまた、白いキャンパスの上に光り輝くものを描こうとした時には、軽く色や明るさで眺めるときにも色や明るさでグラデーションを付けると、白のキャンパスや白の油絵の具以上の明るさや輝きを表現することができます。…覚えておくと、これからあなたの表現力を豊かにするワザになるかもしれません。
そしてまた、白いキャンパスの上に光り輝くものを描こうとした時には、軽く色や明るさで眺めるときにも色や明るさでグラデーションを付けると、白のキャンパスや白の油絵の具以上の明るさや輝きを表現することができます。…覚えておくと、これからあなたの表現力を豊かにするワザになるかもしれません。