雑学界の権威・平林純の考える科学

　少女マンガの定番ストーリーに、「ヒロインが眼鏡を外すと美人になる」というものがありました。 つまり、自分をブサイクだと思っている（あるいは周りから思われている）メガネを掛けたヒロインが、メガネを外した途端に美しく輝く、という鉄板展開です。

　そんな「メガネをとると美人になる」現象は、奇想天外なマンガの中だけの話かと思いきや、実は（「ホンマでっか？」的に）真実です。 「めがねっこ大好き。~ めがねを外すと美人になるは本当か!?」で行った研究報告のように、近視用メガネを掛けた人は、（メガネのレンズ効果によって）目を小さく見えてしまうためブサイクに見えやすく、メガネをとることで（対的に美人に見えるという現象が生じます。

　たとえば、下の画像は

• 伊達メガネを掛けた女性
• -1.0D（ディオプシー）の近視用メガネを掛けた女性

の（処理合成した）顔写真です。近視用メガネを掛けると遠目にも（瞳が小さく見え）ブサイクに見えてしまうことがわかります。

　

　近視の人が凹レンズである眼鏡をかけた場合には、その人の目が他の人からは小さく見えてしまう。実世界でも、少女マンガの世界でも大きな瞳は美少女の象徴であるが、近視の人が眼鏡をかけると、大きな瞳を持つ美少女でも小さな瞳になってしまうのである。近視の人の割合は国によって大きく違うというが、少なくとも現代の日本では近視の人の割合は圧倒的に多い。そんな近視の人が多い日本では「めがねを掛けることで目が小さく見えていた人が、メガネを外した途端お目々パッチリの美人になる」という現象はが起きやすい。つまり、「めがねを外すと美人になる」は実際に起こる現象なのである。

「めがねっこ大好き。~ めがねを外すと美人になるは本当か!?」

　しかし、「メガネをとると美人になる」現象の秘密は、実はこれだけではありません。 サイズが合わない近視用のメガネを掛けていると、目の間隔が妙に離れて平目顔に（外見上）見えてしまったり・目の感覚が過剰に狭まってプロポーションが悪いブサイク顔に見えてしまう…という現象もさらに起きてしまいます。近視用メガネをかけた人を眺めると、メガネレンズの内側にあるものが「小さく」縮小されて見えるのですが、縮小される時の中心位置はレンズ中心位置となります。
　すると、目の位置とレンズ中心位置が一致していないと、目が縮小されて見えるのと同時に、目の位置も移動して見えてしまうのです（参考：右図）。その結果、両レンズの大きさ・間隔が「本当の両目間距離」と違う”サイズが合っていない”メガネを掛けてしまうと、平目顔や寄り目顔といったブサイク顔に見えてしまいます。

　たとえば、下の写真は

• -1.0D（ディオプシー）の近視用メガネを掛けた女性
• メガネを外した女性

の（処理合成した）顔写真です。”サイズが合っていない”近視用メガネを掛けているとブサイクに見えてしまっていて、そのメガネを外すと美しく見えることがわかると思います。奇妙だった両目の間隔も自然なプロポーションになり、縮小されて見えていた瞳も大きくなり、まさに美人度がアップしています。

　

　近視用メガネは「瞳を小さく」見せるだけでなく、サイズが合っていないことにより「ブサイクな平目顔や寄り目顔」に見せてしまいます。 「メガネをとると美人になる」現象は、奇想天外なマンガの中だけの話かと思いきや…実は驚くべきかな真実だったのです。

　駅からどこか目的地に向かうときには、時間があれば「歩く」ものですし、時間がなくて急いでいるような場合には「走る」ものです。…それでは、どのくらい急いでいれば、「歩き」から「走る」に変わるものなのでしょう？つまり、「歩く」と「走る」の境界線は、どのくらいの「速さ（どのくらい時間がなくて急いでいる）」にあるのでしょうか。

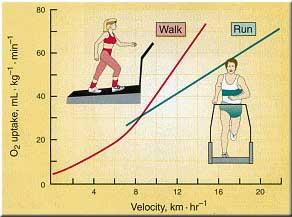　右のグラフは人が歩いたり走ったりする時の、移動速度（km/h）と体重あたり酸素消費量（ml / kg / min）を示したものです。わたしたちは酸素を吸ってエネルギーを生み出すのですから、つまりこのグラフは、わたしたちが歩いたり走ったりする時の、移動速度と消費エネルギーを示したものです。

　このグラフを眺めてみると、時速が約８ｋｍより遅いのであれば歩く方が仕事率が高いし（効率が良い）、それより早い（急いでいる）のであれば歩くより走った方が効率が高くなる、ということがわかります。つまり、効率よく・楽に移動しようと思ったら、移動速度が時速８ｋｍより遅くても間に合うようであれば歩いた方がいいし、それより急がないとダメなようであれば走った方が楽であるわけです。だから、もしも「歩くべきか、それとも、走るべきか…？」とハムレットが悩んでいたとしたら、「それはキミ、歩くと走るの境界線は時速８ｋｍだよ」と教えてあげれば良い、ということになります。

　ちなみに、「早く歩く」といえば競歩です。競歩の速さは、時速１５ｋｍくらいだと言います。エネルギー消費量のグラフを眺めてみると、競歩はランニングより遙かにエネルギーを消費するシンドイ競技だ！ということも実感できるはずです。時速８ｋｍの「歩くべきか走るべきか？の境界線」を超えて、「走った方がずっと楽なのに、そこをガマンしてシンドく歩き続けている」…それが競歩という競技だったのです。

　お風呂に水を入れる時には、（入浴の際に）浴槽から湯がこぼれてしまうことがないように、少なめに水を入れます。 しかし、「（どれくらい）少なめに水（湯）を入れるか」は、あまり意識していないのではないでしょうか？

　浴槽に入ったお湯に体を浸けていくと、（頭の大きさを無視するといった大雑把に考えるなら）「体の体積に相当する高さ分だけ、湯面が上昇」します。 体の密度は（これまた大雑把に言えば）だいたい水と同じくらいということを考えれば、これは「体重に相当する（水の量の）高さ分だけ、湯面が上昇する」と言い換えることもできます。

　単純な計算をすると、「体重(kg)÷浴槽面積（m^2）÷10」という公式で求められる結果数値が、「あなたがお風呂に入った時の湯面上昇高さ（ｃｍ）」を表していることがわかります。 たとえば「70cm × 80cm」の大きさの浴槽の場合、体重６０ｋｇの人であれば、６０÷（0.7 × 0.8）÷10　≒１１cm だけ、お風呂の湯につかった時に湯面が上になります。

　あるいは、もしも体重１５０ｋｇだというマツコ・デラックスさんが、その「70cm × 80cm」の浴槽面積のお風呂に入るなら、マツコさんがお湯に体を入れた瞬間に、150 ÷（0.7 × 0.8）÷10　≒ 27 cmだけ湯面が上昇する、というわけです。

　こんな風に、浴槽面積を知っておけば、自分が浴槽に入ったときにどれだけ湯面が上がるかわかるわけですから、「ちょうど良い量」の水（湯）を浴槽に入れることができ、水やガス代をムダにすることなく、お得でエコな節約ができます。

　そしてまた、
　体重(kg)÷浴槽面積（m^2）÷10 ≒ 湯面上昇高さ（ｃｍ）
という公式を変形すれば、
　体重(kg) ≒１０×浴槽面積（m^2）×湯面上昇高さ（ｃｍ）
という公式にもなりますから、「湯面上昇を眺めれば、あなたの体重がわかってしまう！」ということにもなります。浴槽に毎日の湯面を記録すれば…体重推移がわかってしまったりもするわけです。

「体重(kg)÷浴槽面積（m^2）÷10＝湯面高差（cm）」というエコでお得な節約公式を覚えれば、お財布の中身は膨らんでいき、さらに（体重を意識することで）膨らみがちのお腹の肉は引き締まり痩せていくかも…しれません。