(2013年)2月15日、ロシア南部のウラル地方に隕石(いんせき)が降ってきました。
まぶしく輝き、白い跡を残しつつ空を斜めに横切り飛んでいくさまは、まるで映画の1シーンです。
 ところで、今回の隕石に限らず、小天体が地球の大気に衝突して生み出される流れ星は、横斜めに長く飛んでいくイメージがあります。
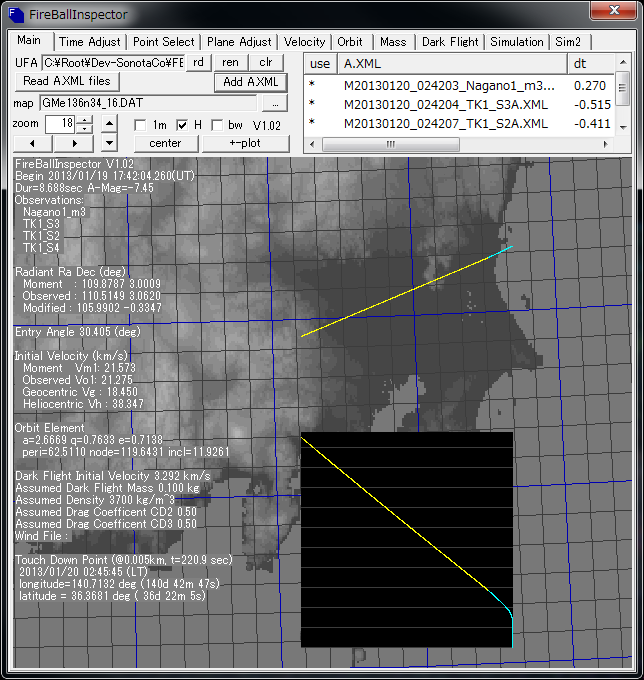
たとえば、(2013年)1月20日に関東を照らした流れ星も、関東平野西部から茨城県の東の海上まで、100km近くの距離を大きく横切っていきました。
そんな風に、流れ星・隕石は「空を斜めに横切る」という印象があります。
ところで、今回の隕石に限らず、小天体が地球の大気に衝突して生み出される流れ星は、横斜めに長く飛んでいくイメージがあります。
たとえば、(2013年)1月20日に関東を照らした流れ星も、関東平野西部から茨城県の東の海上まで、100km近くの距離を大きく横切っていきました。
そんな風に、流れ星・隕石は「空を斜めに横切る」という印象があります。
地球と小天体が衝突する時のことを考えてみます。(地球の自転を無視すると)もしも、小天体が地球の中心に向かってきたら、地球上のどこか一点で「真上から隕石が降ってくる」ことになります。
つまり、隕石が地球に正面衝突する状態です。
そして、隕石が地球と正面衝突するのではなくて、少しズレてぶつかる場合には、隕石は地球の大気に斜めに入ってくることになります。
つまり、空を斜めに横切る流れ星・隕石になるわけです。
その隕石が地球と衝突する際の角度(の頻度分布)を計算してみると、流れ星・隕石が大気にぶつかる角度(頻度)は次式になります。
衝突角度の頻度∝Cos[角度] Sin[角度]
 この式を簡単に言うと、地球に正面衝突(角度=0°)する確率は低く・ずれた衝突をする確率は高いけれど(地球の中心以外の部分にぶつかれば良いのですから)、「角度あたり頻度」に換算すると(ほんの少し衝突位置がずれると衝突角度が大きく変わるので)限りなく横から(角度=90°)ぶつかる確率も低い、という関係を表した式です。
この式を簡単に言うと、地球に正面衝突(角度=0°)する確率は低く・ずれた衝突をする確率は高いけれど(地球の中心以外の部分にぶつかれば良いのですから)、「角度あたり頻度」に換算すると(ほんの少し衝突位置がずれると衝突角度が大きく変わるので)限りなく横から(角度=90°)ぶつかる確率も低い、という関係を表した式です。
その結果、流れ星・隕石は大気に対して斜めにぶつかってくることが一番多く、最も確率が高い角度は「斜め45°」ということになります。
すると、たとえば大気の厚みを100kmとすれば、地球への鉛直距離100kmを落ちる間に、大気に対して斜め45°に侵入してきた隕石は約100km強ほど横方向にも飛んでいきます(すごく単純に言えば、単なる2等辺3角形ですからね)。
こんな計算をしてみると、流れ星や隕石が「斜めに大きく横切っていく」というイメージは現実を反映していそうだ、と気づかされます。
そして、関東を100kmにわたり横切っていった流星の軌跡も、何だか当たり前の普通なことに感じられます。
ところで、普通の流れ星は一瞬しか見えないので(星が流れている間に)願いごとを祈ることはできません。
…今回のロシアの隕石のような少しの間見える「巨大流れ星」だったなら祈ることができるでしょうか?…いやいや、恐怖と驚きとで、とても願いごとを祈る余裕なんて無さそうですね。(関連記事:あなたと見たい、流星群 ~ 同じ流星が見える距離)
 建築基準法とミニスカートの幾何学による「35cm丈のミニスカートは絶対安全」という証明で、「階段の上をいる女性のスカートの内部が見えるか・見えないか」について考えました。そして、建築基準法施行令にもとづくと、公共の場所における階段の角度は上限で35度となり、さらに35度以下の階段では「(偶然、階段の角度と同じ数値である)35cm丈より長いスカートであれば、スカート内部の下着を覗かれてしまうことはない」という証明をしました。
建築基準法とミニスカートの幾何学による「35cm丈のミニスカートは絶対安全」という証明で、「階段の上をいる女性のスカートの内部が見えるか・見えないか」について考えました。そして、建築基準法施行令にもとづくと、公共の場所における階段の角度は上限で35度となり、さらに35度以下の階段では「(偶然、階段の角度と同じ数値である)35cm丈より長いスカートであれば、スカート内部の下着を覗かれてしまうことはない」という証明をしました。
さて、階段ではなくエスカレータならどうなるのでしょう?
私たちが街中にある駅やショッピングセンターといった場所でフロアー間を移動する時には、階段でなくエスカレータを使うことも多いものです。階段の上なら35cm丈のスカートで大丈夫と言われても、さてエスカレータ上ではどうなるのか?という疑問が沸いてきます。
そこで、今回はミニスカートの幾何学でエスカレータ上のミニスカート女性を考えてみることにします。
 実は、エスカレータ上でも「35cm丈のミニスカート=絶対安全となる境界値」なのです。
なぜかというと、階段と同じくエスカレータの勾配にも上限が定められているからです。
建築基準法 施行令129条の12ではエスカレータの勾配は最大で30度となっています。ただし、建設省告示によって、エスカレータの速度が30m以下で揚程6m以下といったいくつかの条件を満たす場合には35度まで許されています。
つまり、公共の場所に存在する可能性のあるエスカレータの最大勾配は(建築基準法施行令で定められている)階段の最大勾配と同じだったのです。
実は、エスカレータ上でも「35cm丈のミニスカート=絶対安全となる境界値」なのです。
なぜかというと、階段と同じくエスカレータの勾配にも上限が定められているからです。
建築基準法 施行令129条の12ではエスカレータの勾配は最大で30度となっています。ただし、建設省告示によって、エスカレータの速度が30m以下で揚程6m以下といったいくつかの条件を満たす場合には35度まで許されています。
つまり、公共の場所に存在する可能性のあるエスカレータの最大勾配は(建築基準法施行令で定められている)階段の最大勾配と同じだったのです。
すると、「勾配角度」と「中身を覗かれないためのスカート丈条件」を三角関数を通じて結びつけるミニスカートの幾何学により、角度上限が35度以下のエスカレータでは「35cm丈より長いスカートであれば、スカート内部の下着を覗かれてしまうことはない」ということがわかるので、結局のところ、エスカレータ上では35cm丈スカートなら安全だということになるわけです。
階段の場合と同じくエスカレータの場合でも、女性のミニスカートの内側を建築基準法が実は守っていたなんて、とても面白いと思いませんか?決まりの秘密に少しの科学を振りかけてみると、意外に興味深い答が出てきたりするのです。
 「シリンダー錠の仕組み」が右の画像です。この種類のシリンダー錠は詳しくはピンタンブラー錠と呼ばれ、鍵が挿されていない状態では、(鍵を入れた際に回転する)内筒と(外側部分の)外筒の間に「ピン」が刺さっていて、内筒は回転しない(=鍵が開かない)状態になっています。たとえば、合っていない鍵を内筒に差し入れ・回そうとしても、ピンが外筒と内筒の間で挟まっていますから、そのピンが折れたりしない限りは回りません。しかし、鍵を差し込むと、ピンの分離部分が内筒と外筒の境目に動かされて、刺さった鍵を回すことで内筒が回転する(=鍵が開く)状態になるわけです。
「シリンダー錠の仕組み」が右の画像です。この種類のシリンダー錠は詳しくはピンタンブラー錠と呼ばれ、鍵が挿されていない状態では、(鍵を入れた際に回転する)内筒と(外側部分の)外筒の間に「ピン」が刺さっていて、内筒は回転しない(=鍵が開かない)状態になっています。たとえば、合っていない鍵を内筒に差し入れ・回そうとしても、ピンが外筒と内筒の間で挟まっていますから、そのピンが折れたりしない限りは回りません。しかし、鍵を差し込むと、ピンの分離部分が内筒と外筒の境目に動かされて、刺さった鍵を回すことで内筒が回転する(=鍵が開く)状態になるわけです。
しかし、こうしたシリンダー錠は、正しい鍵がなくても簡単に鍵を開けられてしまいます。
それは、たとえば、

- まず、内筒に何かを差し入れて、内筒を回転させようとする力をかけてみます。すると、「内筒が回転しないように止めているピン」に力がかかります。しかし、たとえば右側の画像ではピンは7本ありますが、ピンの太さといったものにはバラツキがありますから、実は「内筒が回転しないように止めているのは「(最もジャマになっている)1本のピン」だけです
- 内筒の中のピンを軽く押していくと、「(最も邪魔になっている)1本のピン」には力がかかっているので、「邪魔ピンはこれ」とわかります
- そして、邪魔ピンを動かすと、邪魔ピンの分離部分が内筒と外筒の境目に動かされた瞬間に内筒が少し周り、邪魔ピンは邪魔ではなくなり・(内筒が少し回転してしまっていますから)その位置から戻らなくなります
- すると、今度は他のピンが「邪魔ピン」になり、その邪魔ピンを同じように見つけ・動かしていくと、最後には全部のピンが突破され、鍵は開いてしまう
というようなやり方です。
このやり方は、「鍵が開く・開かないを決めている部分に力などがかかった際の”動きの違い”」を利用して、鍵を開けています。実は、シリンダー錠に限らず、ダイヤル錠など他の種類の鍵でも、このやり方で鍵が開けられてしまうことは多いものです。たとえば、ダイヤル錠を手に持ち、鍵が開くように引っ張りながらダイヤルを回転させると、正しい位置にダイヤルが来た瞬間に動かなくなり、それを繰り返すと鍵は開いてしまいます。
こうした開け方、つまり「鍵が開く・開かないを決めている部分に力などがかかった際の”動きの違い”」を利用した鍵の破り方は、「物理的な鍵」でだけ当てはまるやり方ではないか?と思われるかもしれません。つまり、たとえばコンピュータのパスワードチェックなら”動きの違い”なんて外側から知ることはできず、パスワード破りなんてできないのではないか?と思われたりするかもしれません。
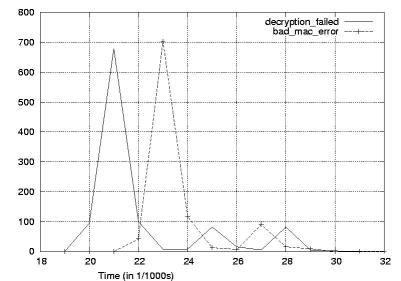 しかし、コンピュータでも「鍵が開く・開かないを決めている部分に力などがかかった際の”動きの違い”」を利用して、パスワード破りがされてしまうことがあります。たとえば、「パスワードが合っているか」を判定するソフトウェアが、「入力パスワード中の間違っている文字数」などによって処理時間が異なってしまう場合には、処理時間を計ることでパスワードを破ることができてしまったりします(参考:パスワードの判定にstrcmpを使うべきでない理由)。具体的には、パスワード認証システムに対してパスワードをデタラメに入れたとき、もしも1文字目が間違っていたらそこで「パスワードが間違ってる」と「すぐに処理が終わる」けれど、もしも1文字目が合っていたら次の2文字目が合っているかの確認をしなければならないので(間違っている場合より)文字が合っている場合は余計に時間がかかり、その時間差を手がかりにすれば「あっ、今入れた文字は合ってるんだ」とわかるというわけです。そして、それを繰り返していくと、パスワードを破ることができる…なんていうことも、場合によっては起こりうることになります。
しかし、コンピュータでも「鍵が開く・開かないを決めている部分に力などがかかった際の”動きの違い”」を利用して、パスワード破りがされてしまうことがあります。たとえば、「パスワードが合っているか」を判定するソフトウェアが、「入力パスワード中の間違っている文字数」などによって処理時間が異なってしまう場合には、処理時間を計ることでパスワードを破ることができてしまったりします(参考:パスワードの判定にstrcmpを使うべきでない理由)。具体的には、パスワード認証システムに対してパスワードをデタラメに入れたとき、もしも1文字目が間違っていたらそこで「パスワードが間違ってる」と「すぐに処理が終わる」けれど、もしも1文字目が合っていたら次の2文字目が合っているかの確認をしなければならないので(間違っている場合より)文字が合っている場合は余計に時間がかかり、その時間差を手がかりにすれば「あっ、今入れた文字は合ってるんだ」とわかるというわけです。そして、それを繰り返していくと、パスワードを破ることができる…なんていうことも、場合によっては起こりうることになります。
また、コンピュータはソフトウェアで動いているといっても、ソフトウェアは結局のところハードウェア装置上で動いていますから、「鍵が開く・開かないを決めている部分に力などがかかった際の”動きの違い”」が装置の消費電力や(外部に放出する)電磁波や音波などに現れてしまうこともあります。つまり、装置の状態を観察しながらパスワード認証をさせてみると「入れたパスワードが合っている度合い」がわかってしまったりする可能性もあるのです。
シリンダー錠の開け方と同じように、コンピュータのパスワードも破られてしまうというのは、何だか少し意外で興味深く感じられるはないでしょうか。
 ところで、今回の隕石に限らず、小天体が地球の大気に衝突して生み出される流れ星は、横斜めに長く飛んでいくイメージがあります。
たとえば、(2013年)1月20日に関東を照らした流れ星も、関東平野西部から茨城県の東の海上まで、100km近くの距離を大きく横切っていきました。
そんな風に、流れ星・隕石は「空を斜めに横切る」という印象があります。
ところで、今回の隕石に限らず、小天体が地球の大気に衝突して生み出される流れ星は、横斜めに長く飛んでいくイメージがあります。
たとえば、(2013年)1月20日に関東を照らした流れ星も、関東平野西部から茨城県の東の海上まで、100km近くの距離を大きく横切っていきました。
そんな風に、流れ星・隕石は「空を斜めに横切る」という印象があります。
 この式を簡単に言うと、地球に正面衝突(角度=0°)する確率は低く・ずれた衝突をする確率は高いけれど(地球の中心以外の部分にぶつかれば良いのですから)、「角度あたり頻度」に換算すると(ほんの少し衝突位置がずれると衝突角度が大きく変わるので)限りなく横から(角度=90°)ぶつかる確率も低い、という関係を表した式です。
この式を簡単に言うと、地球に正面衝突(角度=0°)する確率は低く・ずれた衝突をする確率は高いけれど(地球の中心以外の部分にぶつかれば良いのですから)、「角度あたり頻度」に換算すると(ほんの少し衝突位置がずれると衝突角度が大きく変わるので)限りなく横から(角度=90°)ぶつかる確率も低い、という関係を表した式です。






