201301.19
「シリンダー錠の開け方」で知る「コンピュータ・パスワード破りの秘密」!?
「シリンダー錠の仕組み」が右の画像です。この種類のシリンダー錠は詳しくはピンタンブラー錠と呼ばれ、鍵が挿されていない状態では、（鍵を入れた際に回転する）内筒と（外側部分の）外筒の間に「ピン」が刺さっていて、内筒は回転しない（＝鍵が開かない）状態になっています。たとえば、合っていない鍵を内筒に差し入れ・回そうとしても、ピンが外筒と内筒の間で挟まっていますから、そのピンが折れたりしない限りは回りません。しかし、鍵を差し込むと、ピンの分離部分が内筒と外筒の境目に動かされて、刺さった鍵を回すことで内筒が回転する（＝鍵が開く）状態になるわけです。
しかし、こうしたシリンダー錠は、正しい鍵がなくても簡単に鍵を開けられてしまいます。
それは、たとえば、
- まず、内筒に何かを差し入れて、内筒を回転させようとする力をかけてみます。すると、「内筒が回転しないように止めているピン」に力がかかります。しかし、たとえば右側の画像ではピンは７本ありますが、ピンの太さといったものにはバラツキがありますから、実は「内筒が回転しないように止めているのは「（最もジャマになっている）１本のピン」だけです
- 内筒の中のピンを軽く押していくと、「（最も邪魔になっている）１本のピン」には力がかかっているので、「邪魔ピンはこれ」とわかります
- そして、邪魔ピンを動かすと、邪魔ピンの分離部分が内筒と外筒の境目に動かされた瞬間に内筒が少し周り、邪魔ピンは邪魔ではなくなり・（内筒が少し回転してしまっていますから）その位置から戻らなくなります
- すると、今度は他のピンが「邪魔ピン」になり、その邪魔ピンを同じように見つけ・動かしていくと、最後には全部のピンが突破され、鍵は開いてしまう
このやり方は、「鍵が開く・開かないを決めている部分に力などがかかった際の”動きの違い”」を利用して、鍵を開けています。実は、シリンダー錠に限らず、ダイヤル錠など他の種類の鍵でも、このやり方で鍵が開けられてしまうことは多いものです。たとえば、ダイヤル錠を手に持ち、鍵が開くように引っ張りながらダイヤルを回転させると、正しい位置にダイヤルが来た瞬間に動かなくなり、それを繰り返すと鍵は開いてしまいます。
こうした開け方、つまり「鍵が開く・開かないを決めている部分に力などがかかった際の”動きの違い”」を利用した鍵の破り方は、「物理的な鍵」でだけ当てはまるやり方ではないか？と思われるかもしれません。つまり、たとえばコンピュータのパスワードチェックなら”動きの違い”なんて外側から知ることはできず、パスワード破りなんてできないのではないか？と思われたりするかもしれません。
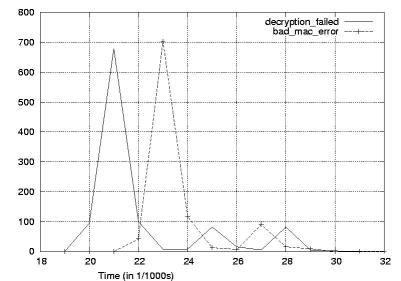しかし、コンピュータでも「鍵が開く・開かないを決めている部分に力などがかかった際の”動きの違い”」を利用して、パスワード破りがされてしまうことがあります。たとえば、「パスワードが合っているか」を判定するソフトウェアが、「入力パスワード中の間違っている文字数」などによって処理時間が異なってしまう場合には、処理時間を計ることでパスワードを破ることができてしまったりします（参考：パスワードの判定にstrcmpを使うべきでない理由）。具体的には、パスワード認証システムに対してパスワードをデタラメに入れたとき、もしも１文字目が間違っていたらそこで「パスワードが間違ってる」と「すぐに処理が終わる」けれど、もしも１文字目が合っていたら次の２文字目が合っているかの確認をしなければならないので（間違っている場合より）文字が合っている場合は余計に時間がかかり、その時間差を手がかりにすれば「あっ、今入れた文字は合ってるんだ」とわかるというわけです。そして、それを繰り返していくと、パスワードを破ることができる…なんていうことも、場合によっては起こりうることになります。
また、コンピュータはソフトウェアで動いているといっても、ソフトウェアは結局のところハードウェア装置上で動いていますから、「鍵が開く・開かないを決めている部分に力などがかかった際の”動きの違い”」が装置の消費電力や（外部に放出する）電磁波や音波などに現れてしまうこともあります。つまり、装置の状態を観察しながらパスワード認証をさせてみると「入れたパスワードが合っている度合い」がわかってしまったりする可能性もあるのです。
シリンダー錠の開け方と同じように、コンピュータのパスワードも破られてしまうというのは、何だか少し意外で興味深く感じられるはないでしょうか。
