201408.22
Excelで”-1^2″の計算結果が1で、”0-1^2″は-1になるヒミツ!?
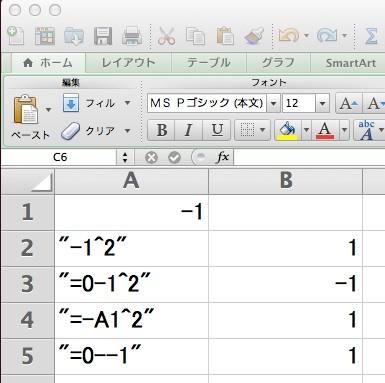
Microsoft Excel で ” - 1 ^ 2 ” を計算すると、なんと「その結果は” 1 “になる!」という話があります。「”-1^2″が”-1″でなく”1”になってしまうなんて!」「演算(子)の優先順位から言って、^すなわち冪乗演算(子)は減算演算(子)より優先されるはず。だから、”-1^2″は”-1″になるはずじゃないか!」「これってトンデモないバグじゃないの!?」とビックリする人もいるかもしれません。…しかし、” - 1 ^ 2 “をExcelで計算した結果がイコール”-1″になるということは、実は「Excelの仕様」として結構有名な話です(Topic: Excel Math Bug, Incorrect order of operations in formula)。
エクセルで”= – 1 ^ 2 “と入力すると、この”-“は「AからBを引く」ということを行う「AとBの間の減算を意味する演算(子)」にはなりません。この”-“は、その”-”の右側にある「A」を修飾する「単項演算子(Unary operator)」として解釈されます。つまり、「Aの符号を反転した数を返す演算子」になります。…こう書くと「なんだそれ?Aの符号を反転した数はゼロからAを引いた数なんだから、結局のところ、ゼロとAの間の減算と同じじゃないか!」と思われるかもしれないですが、Excelは(そして少なからずのプログラミング言語も)「AとBの間の減算を意味する演算(子)」と「Aの符号を反転した数を返す演算子」は違うものとして取り扱われます。そして、Excelは符号を反転する単項演算子を意味する”-“は、優先度が冪乗よりも高く取り扱われるため、”-1^2″=”(-1)*(-1)” ということになり計算結果が1になるのです(XL: Order of Operations in Formulas)。
ちなみに、”=-1^2″とすると計算結果は1になりますが、”=0-1^2″とするとエクセルは”-1″という計算結果を出力します。つまり、”-1^2″と”0-1^2″は違う値を返します。…なぜかと言えば、”-1^2″の”-“は「左側に値や変数がなく、符号を反転する単項演算子として解釈される」のに対して、”0-1^2″の”-“は左側にゼロがあり、ゼロと後続する値の間で減算を行うという減算演算子として解釈されるからです。たとえば、”=0–1″と入力すると、特にエラーが出ることもなく、1という値が返ってきます。この場合は、2個ある”-“のうち最初のものがゼロと後続の値間の減算演算子として解釈され、次の”−”は1の符号を反転する単項演算子として解釈されます。そして、単項演算子としての”-“は冪乗や乗算の演算子より優先度が高く取り扱われますが、減算演算子としての”-“はそれらよりも優先度は低く扱われます。だから、”-1^2″の計算結果は1になるのに対して、”0-1^2″は-1になるというわけです。さらには、”-“を3個でも4個でも問題なく重ねて使うこともできます。たとえば、—-1なら符号反転させる単項演算子4個として解釈され、1—-1なら、減算演算子1個・単項演算子3個の組み合わせ…ということになります
このようなExcelの演算子解釈ルール(優先順位ルール)は、どのようにして生まれたのでしょう?「それは、きっとExcelに先行して発売されていた表計算ソフトのVisicalcやLotus 1-2-3にならったに違いない!」と言われることも多いのですが、残念ながらそうではありません。Visicalcの演算子解釈順は、単純に左から右へと並ぶ”並び順”で解釈されますし、Lotus 1-2-3は(Microsoftのサイトにも、ExcelとLotus 1-2-3の計算順序は違うよ!と書いてありましたが)”-1^2″の計算結果は”-1″を返します(Why is =-1^2 positive and =0-1^2 negative?)。
それではExcelはなぜ「Excelは符号を反転する単項演算子を意味する”-“は、優先度が冪乗よりも高く取り扱う」というルールを採用しているのでしょうか?…「その理由はこうだった!」という確かな理由は定かではありません。しかし、昔からビジネス関連のアプリケーションを書くために非常に頻繁に使われてきたプログラミング言語COBOLの文法にならった…という説が一番説得力があるように思われます。それは、(当時FORTRANなどを使っていた)数式を使うエンジニアではなく、”普通の人”が使うような目的には、一般的な演算子優先順位ではなく・「マイナス1の2乗」と言ったら「(−1)の2乗」の方が自然だよね!というわけで、COBOLなどに習ってExcelの演算子優先順位が決定されたという考え方です。
この「– 2 ^ 2 = + 4 と – 2 ^ 2 = – 4 …一体どちらが”正しい”の!?」という話題はとても面白いものです。知らない人は眺めてみるときっと面白いと思います。