「何人が集まれば、同じ誕生日の人(たち)がいる確率が50%を超えるか?」という問題があります。
計算すると、その答えは「23人」となり、意外に少ない人数でも「同じ誕生日の人たちがいる確率が高い」ので、誕生日のパラドックスと言われたりします。計算自体は、
同じ誕生日の人たちがいる確率=1-同じ誕生日の人たちがいない確率
なので、「同じ誕生日の人たちがいない確率」を誕生日が重ならない条件と考えれば、たとえば23人であれば
=1 – 364/365 × 363/365 × 362/365 …× (365-23 + 1) / 365
=0.50729723432398540723…
と計算することができて、その確率は50パーセントを超えるというわけです(詳しくはたとえばこちら)。
ところで、戦前の日本の月別出生率を眺めると、誕生日が1〜3月に集中していたことがわかります。たとえば、「1899年から2000年までの月別出生率」を見ると、「1月・2月・3月の出生率が他の月の1.5倍くらい高く」「一番出生率が少ない6月と比べると、1〜3月は2倍ほど高い」という具合になっています。(データが途切れてる箇所が太平洋戦争時です)
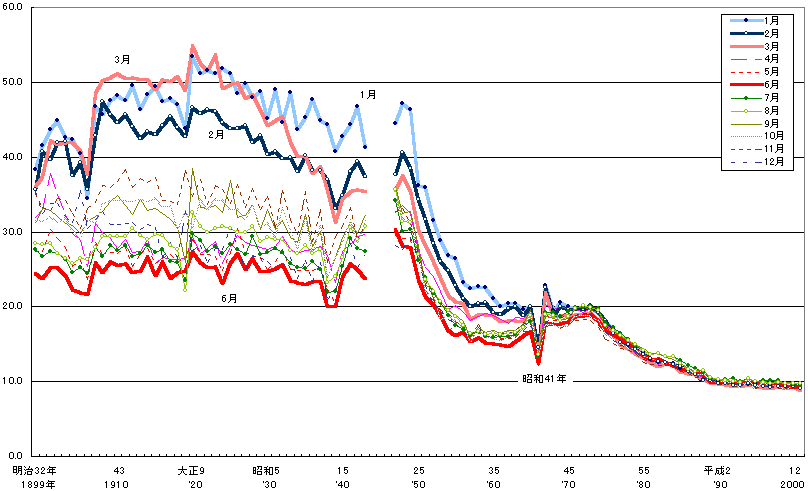
さて問題です。このような誕生日が1〜3月の時期に集中していた戦前の日本で「誕生日のパラドックス」を考えてみると、つまり「何人が集まれば、同じ誕生日の人(たち)がいる確率が50%を超えるか?」を考えてみると、一体どんな答が出てくるでしょう?…真夏の夜に挑戦するのに丁度良い面白いパズルだと思いませんか?直感的には、何人いれば同じ誕生日の人たちがいる確率が50%を超えると思いますか?

