（2013年）2月15日、ロシア南部のウラル地方に隕石（いんせき）が降ってきました。
まぶしく輝き、白い跡を残しつつ空を斜めに横切り飛んでいくさまは、まるで映画の１シーンです。
ところで、今回の隕石に限らず、小天体が地球の大気に衝突して生み出される流れ星は、横斜めに長く飛んでいくイメージがあります。
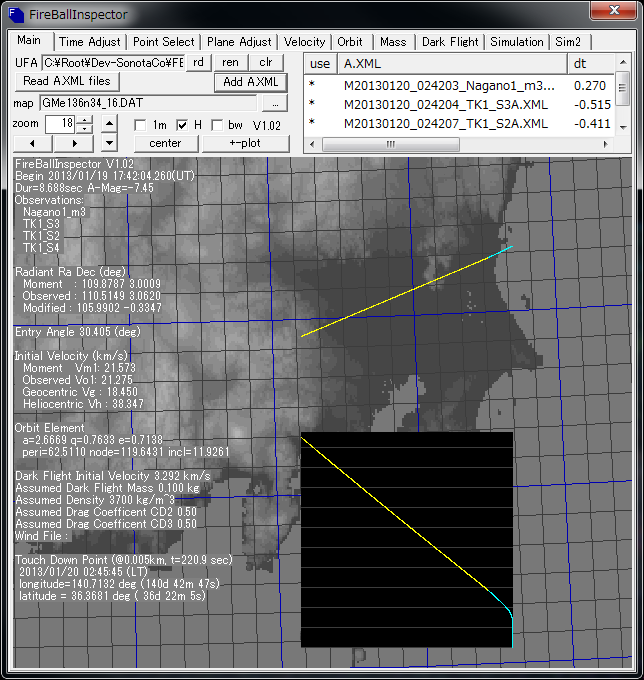
たとえば、（2013年）1月20日に関東を照らした流れ星も、関東平野西部から茨城県の東の海上まで、100km近くの距離を大きく横切っていきました。
そんな風に、流れ星・隕石は「空を斜めに横切る」という印象があります。
地球と小天体が衝突する時のことを考えてみます。（地球の自転を無視すると）もしも、小天体が地球の中心に向かってきたら、地球上のどこか一点で「真上から隕石が降ってくる」ことになります。
つまり、隕石が地球に正面衝突する状態です。
そして、隕石が地球と正面衝突するのではなくて、少しズレてぶつかる場合には、隕石は地球の大気に斜めに入ってくることになります。
つまり、空を斜めに横切る流れ星・隕石になるわけです。
その隕石が地球と衝突する際の角度（の頻度分布）を計算してみると、流れ星・隕石が大気にぶつかる角度（頻度）は次式になります。
衝突角度の頻度∝Cos[角度] Sin[角度]
この式を簡単に言うと、地球に正面衝突（角度＝０°）する確率は低く・ずれた衝突をする確率は高いけれど（地球の中心以外の部分にぶつかれば良いのですから）、「角度あたり頻度」に換算すると（ほんの少し衝突位置がずれると衝突角度が大きく変わるので）限りなく横から（角度＝９０°）ぶつかる確率も低い、という関係を表した式です。
その結果、流れ星・隕石は大気に対して斜めにぶつかってくることが一番多く、最も確率が高い角度は「斜め４５°」ということになります。
すると、たとえば大気の厚みを１００ｋｍとすれば、地球への鉛直距離１００ｋｍを落ちる間に、大気に対して斜め４５°に侵入してきた隕石は約１００ｋｍ強ほど横方向にも飛んでいきます（すごく単純に言えば、単なる２等辺３角形ですからね）。
こんな計算をしてみると、流れ星や隕石が「斜めに大きく横切っていく」というイメージは現実を反映していそうだ、と気づかされます。
そして、関東を１００ｋｍにわたり横切っていった流星の軌跡も、何だか当たり前の普通なことに感じられます。
ところで、普通の流れ星は一瞬しか見えないので（星が流れている間に）願いごとを祈ることはできません。
…今回のロシアの隕石のような少しの間見える「巨大流れ星」だったなら祈ることができるでしょうか？…いやいや、恐怖と驚きとで、とても願いごとを祈る余裕なんて無さそうですね。（関連記事：あなたと見たい、流星群 ~ 同じ流星が見える距離）
名画の中には、描かれるものの配置が計算し尽くされたかのように見えるものが数多くあります。たとえば、右のフェルメールが描いた油絵 “Die Malkunst” は、画の中に描かれたものすべてが、補助線を引いてみると見事に黄金比（黄金率）に沿っていることがわかります（左図：黄金比配置を示した補助線テンプレート、右図：フェルメール “Die Malkunst”）。黄金比というのは、1：(１+√5)/2という比率で、この比に沿う配置は安定感や美しさを強く感じさせることが知られています。フェルメールの “Die Malkunst”は、部屋を飾るカーテン、描かれた女性、画家の体や腕が、すべて美しく黄金比にもとづく配置になっています。
計算され尽くした「名画」は、過去の芸術の中にだけ存在するわけではありません。たとえば、私たちが毎日使うPCにインストールされているマイクロソフトOfficeの中にある、クリップアート画像の数々も、よくよく眺めてみると黄金比に忠実に沿った配置にされていたりします（右図）。海に走る波、波に乗るサーファー、背景に広がる岩場…画像中の素材が綺麗に黄金比に沿った配置になっています。あるいは、青空を背景に立つ鉄骨と、空中を走るローラーコースターが、見事に黄金比に沿った配置となっていることがわかります。
何気なく使うOfficeクリップアートも、数々の名画と同じように、実は計算し尽くされた配置になっていたりします。…そんなことを考えながらOfficeクリップアートを眺めてみれば、Officeでの資料作りも「世界の美術館巡り」に思えてくるかもしれません。
冬の白銀の世界は、美しいと同時に厳しく恐ろしい存在です。
たとえば、ほんの少し吹雪くだけで視界を失ってしまい、全く方向がわからなくなったりします。
吹雪くとき…つまり雪が降り・風が吹く時の視界＝視程は、（実験的に求められた）このような式で表すことができます*。
視程（m）＝10^(-0.886 Log[飛雪空間密度（g/m^3） 速度（m/s）] + 2.648)
上式でとても興味深いのは、視界（視程）が「１立方メートルあたりに存在する雪の重量（飛雪空間密度）」と同じくらい「雪の速度」に影響を受ける、ということです。
つまり、たとえば風速（雪を動かす風）が２倍増すと、あたかも目の前を舞う雪の量が２倍増えたのと同じ影響がある、ということになります。下の２枚のグラフは、
- 左：雪が秒速35cmで降っているとき、雪の量が変わると視界がどうなるか
- 右：雪が１立方メートルあたり１ｇ存在するとき、雪の速度が変わると視界がどうなるか
を示したものです。雪粒子の量が増えると視界は悪くなるのは当然ですが、雪粒子が早く動くようになると、それでも同じように目の前の視界が失われてしまうことがわかります。
しんしんと静かに美しく降る粉雪も、ほんの少しの風が吹き始めただけで、視界を失わせる吹雪へと姿を変えてしまいます。吹雪中での視界距離の式を見ると、雪を舞わせる風の怖さを実感するのではないでしょうか。
＊吹雪時に人間が感じる視程と視程計や吹雪計による計測値との関係（武知ら）
この式を簡単に言うと、地球に正面衝突（角度＝０°）する確率は低く・ずれた衝突をする確率は高いけれど（地球の中心以外の部分にぶつかれば良いのですから）、「角度あたり頻度」に換算すると（ほんの少し衝突位置がずれると衝突角度が大きく変わるので）限りなく横から（角度＝９０°）ぶつかる確率も低い、という関係を表した式です。
