雑学界の権威・平林純の考える科学

　少女マンガの定番ストーリーに、「ヒロインが眼鏡を外すと美人になる」というものがありました。 つまり、自分をブサイクだと思っている（あるいは周りから思われている）メガネを掛けたヒロインが、メガネを外した途端に美しく輝く、という鉄板展開です。

　そんな「メガネをとると美人になる」現象は、奇想天外なマンガの中だけの話かと思いきや、実は（「ホンマでっか？」的に）真実です。 「めがねっこ大好き。~ めがねを外すと美人になるは本当か!?」で行った研究報告のように、近視用メガネを掛けた人は、（メガネのレンズ効果によって）目を小さく見えてしまうためブサイクに見えやすく、メガネをとることで（対的に美人に見えるという現象が生じます。

　たとえば、下の画像は

• 伊達メガネを掛けた女性
• -1.0D（ディオプシー）の近視用メガネを掛けた女性

の（処理合成した）顔写真です。近視用メガネを掛けると遠目にも（瞳が小さく見え）ブサイクに見えてしまうことがわかります。

　

　近視の人が凹レンズである眼鏡をかけた場合には、その人の目が他の人からは小さく見えてしまう。実世界でも、少女マンガの世界でも大きな瞳は美少女の象徴であるが、近視の人が眼鏡をかけると、大きな瞳を持つ美少女でも小さな瞳になってしまうのである。近視の人の割合は国によって大きく違うというが、少なくとも現代の日本では近視の人の割合は圧倒的に多い。そんな近視の人が多い日本では「めがねを掛けることで目が小さく見えていた人が、メガネを外した途端お目々パッチリの美人になる」という現象はが起きやすい。つまり、「めがねを外すと美人になる」は実際に起こる現象なのである。

「めがねっこ大好き。~ めがねを外すと美人になるは本当か!?」

　しかし、「メガネをとると美人になる」現象の秘密は、実はこれだけではありません。 サイズが合わない近視用のメガネを掛けていると、目の間隔が妙に離れて平目顔に（外見上）見えてしまったり・目の感覚が過剰に狭まってプロポーションが悪いブサイク顔に見えてしまう…という現象もさらに起きてしまいます。近視用メガネをかけた人を眺めると、メガネレンズの内側にあるものが「小さく」縮小されて見えるのですが、縮小される時の中心位置はレンズ中心位置となります。
　すると、目の位置とレンズ中心位置が一致していないと、目が縮小されて見えるのと同時に、目の位置も移動して見えてしまうのです（参考：右図）。その結果、両レンズの大きさ・間隔が「本当の両目間距離」と違う”サイズが合っていない”メガネを掛けてしまうと、平目顔や寄り目顔といったブサイク顔に見えてしまいます。

　たとえば、下の写真は

• -1.0D（ディオプシー）の近視用メガネを掛けた女性
• メガネを外した女性

の（処理合成した）顔写真です。”サイズが合っていない”近視用メガネを掛けているとブサイクに見えてしまっていて、そのメガネを外すと美しく見えることがわかると思います。奇妙だった両目の間隔も自然なプロポーションになり、縮小されて見えていた瞳も大きくなり、まさに美人度がアップしています。

　

　近視用メガネは「瞳を小さく」見せるだけでなく、サイズが合っていないことにより「ブサイクな平目顔や寄り目顔」に見せてしまいます。 「メガネをとると美人になる」現象は、奇想天外なマンガの中だけの話かと思いきや…実は驚くべきかな真実だったのです。

　お風呂に水を入れる時には、（入浴の際に）浴槽から湯がこぼれてしまうことがないように、少なめに水を入れます。 しかし、「（どれくらい）少なめに水（湯）を入れるか」は、あまり意識していないのではないでしょうか？

　浴槽に入ったお湯に体を浸けていくと、（頭の大きさを無視するといった大雑把に考えるなら）「体の体積に相当する高さ分だけ、湯面が上昇」します。 体の密度は（これまた大雑把に言えば）だいたい水と同じくらいということを考えれば、これは「体重に相当する（水の量の）高さ分だけ、湯面が上昇する」と言い換えることもできます。

　単純な計算をすると、「体重(kg)÷浴槽面積（m^2）÷10」という公式で求められる結果数値が、「あなたがお風呂に入った時の湯面上昇高さ（ｃｍ）」を表していることがわかります。 たとえば「70cm × 80cm」の大きさの浴槽の場合、体重６０ｋｇの人であれば、６０÷（0.7 × 0.8）÷10　≒１１cm だけ、お風呂の湯につかった時に湯面が上になります。

　あるいは、もしも体重１５０ｋｇだというマツコ・デラックスさんが、その「70cm × 80cm」の浴槽面積のお風呂に入るなら、マツコさんがお湯に体を入れた瞬間に、150 ÷（0.7 × 0.8）÷10　≒ 27 cmだけ湯面が上昇する、というわけです。

　こんな風に、浴槽面積を知っておけば、自分が浴槽に入ったときにどれだけ湯面が上がるかわかるわけですから、「ちょうど良い量」の水（湯）を浴槽に入れることができ、水やガス代をムダにすることなく、お得でエコな節約ができます。

　そしてまた、
　体重(kg)÷浴槽面積（m^2）÷10 ≒ 湯面上昇高さ（ｃｍ）
という公式を変形すれば、
　体重(kg) ≒１０×浴槽面積（m^2）×湯面上昇高さ（ｃｍ）
という公式にもなりますから、「湯面上昇を眺めれば、あなたの体重がわかってしまう！」ということにもなります。浴槽に毎日の湯面を記録すれば…体重推移がわかってしまったりもするわけです。

「体重(kg)÷浴槽面積（m^2）÷10＝湯面高差（cm）」というエコでお得な節約公式を覚えれば、お財布の中身は膨らんでいき、さらに（体重を意識することで）膨らみがちのお腹の肉は引き締まり痩せていくかも…しれません。

　「大変な・ツラい場所」のシンボルとして扱われる場所のひとつが「宇宙」です。たとえば、地上を遙かに離れた宇宙空間には空気も（ほとんど）なく、人間が生きていける環境ではありません。そして、もうひとつの「大変な・ツラい場所」のシンボルが「大阪湾」です。大阪湾もやはり人間には辛い環境なので、（重しを付けられ）大阪湾に沈められてしまったりすると、私たちは生きていけないに違いありません。

　そんな、大変な場所「宇宙」と「大阪湾」に炭酸ペットボトルとドラム缶を派遣してみたら、一体どんなことになるでしょうか？たとえば、使い終わった（中身が空になった）炭酸ペットボトルを宇宙（真空）中に放り出したらペットボトルはどうなるのでしょう？ また、大阪湾に（巨大な重しでも付けブクブクと）ドラム缶を沈めてみたら、ドラム缶は一体どうなるのでしょうか。

　炭酸ペットボトルを宇宙（真空）中に放り出すと、ペットボトルには容器内部の圧力と外部の圧力の差による力が働きます。 ペットボトル内部にある空気は１気圧で、外は真空で気圧はゼロということは、気圧差にして１気圧分に相当する力が内側から外側に向かって働くことになります。 しかし、炭酸ペットボトルは（炭酸飲料を中に入れている状態で破裂したりすることがないように）数気圧以上の耐圧性能を持っています。 ペットボトル外側より内側の方が圧力が高い限りは、ボトル内外で数気圧の圧力差があっても壊れることはありません（だから、ペットボトルロケットだって作ることができるのです）。 ということは、炭酸ペットボトルを宇宙（空間）に放り出したとしても、たかだか１気圧程度の圧力差では、ペットボトルは壊れたりすることはない、ということになります。

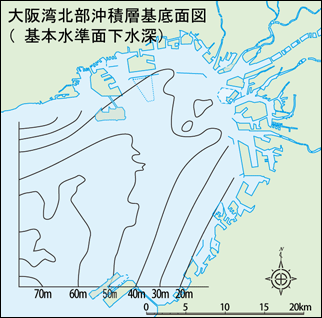　さて、大阪湾にドラム缶を沈めたら、一体どういうことが起きるでしょうか？ 大阪湾の水深データベースを見ると、大阪湾は陸地から少し離れると、すぐに水深１０数メートル程度になります。 海中の水圧は、水深１０ｍでほぼ１気圧に相当します。 つまり、大阪湾に重しを付けた空ドラム缶を沈めると、そのドラム缶に対して外から内側に向かって１気圧以上の水圧がかかることになります。

　ところが、ドラム缶は外から押される力には意外なほど弱いものです。 金属で頑丈に作られたように見えるドラム缶も、もしもドラム缶の中から空気を吸ったりすることでドラム缶の内側の方が外側より１気圧だけ低いような状態にすると、ドラム缶はその圧力に耐えきれず潰れてしまいます。 たとえば、下の動画のように、熱い水蒸気で満ちたドラム缶に封をした後にドラム缶を水で冷やしたりすると、ドラム缶内部の気圧が下がり、ドラム缶の外側にある１気圧の大気圧によってぺしゃんこになってしまいます。

　というわけで、「宇宙（真空）に放り出した炭酸ペットボトル」と「大阪湾に沈めたドラム缶」…壊れたのは「大阪湾に沈めたドラム缶」でした。この答は当たり前だったでしょうか？それとも少し意外な答えだったでしょうか？