雑学界の権威・平林純の考える科学

　とても面白いことが、単純な算数を使うだけで導き出されることが数多くあります。 たとえば、以前書いたように、「３５ｃｍ丈のミニスカートは絶対安全という証明」を簡単な算数（数学）を使うとすることができたりします。

　今回は、「薄着になりがちな真夏に、ブラジャーの中にある胸先が見えてしまうのは、一体どんな条件なのか？」を、誰もが習った「とても単純な算数」を使って導き出してみることにします。

　右上画像は、3/4カップ形状のブラジャーに包まれた「胸のモデル」を描いてみたものです。 ブラジャー中の胸先が「チラリ」見えてしまう現象は、胸とブラジャーの隙間から胸先が見えてしまうとことで起きてしまうものです。そこで、そんな「胸とブラジャーの隙間を通して胸先が見えてしまう条件」について、（右上図に２軸で書き入れた）断面平面を考えて、その平面上で簡単に考えてみましょう。

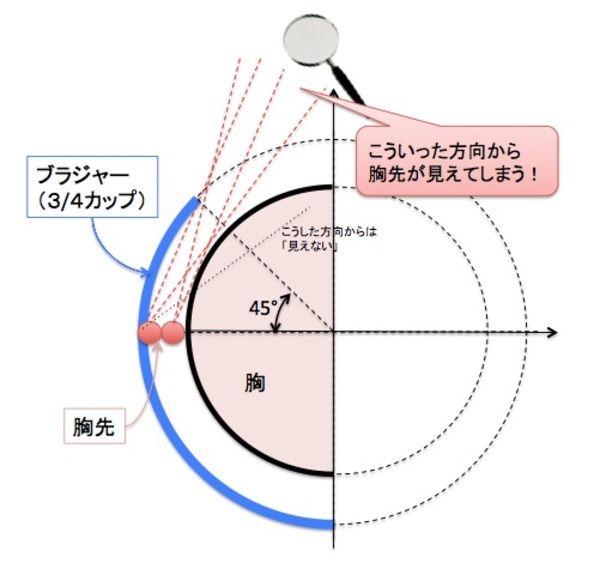　右図が、バスト・3/4カップブラ（青太線）・胸先（朱色の円…円が２つあるのは、特に意味はありません）を描いてみたものです。 向かって右側が胴体側で、この平面図上で言うと、斜め右上から（胸とブラの隙間を通して）胸先が見えてしまっているような状態になっています。

　図を描き・眺めてみれば、胸先が胸とブラの隙間を通し見えてしまう時、その胸先が見える方向は、「胸先とブラのカップの縁を結んだ直線」と「胸先から胸表面に接するように引いた接線」との間の向きだということがわかります。言い換えれば、ブラ・カップ中にある胸先から（他の人の視点位置）に線を引いたとき、その線が「ブラカップの3/4円周の線」とも「胸を形作る半円」とも交わることが無い場合、「胸先チラリ現象が生じてしまう」というわけです。

　さらに、この図を眺めつつ「胸先チラリ現象が生じる・生じないの境界線となる”胸先チラリのギリギリ条件”」を考えてみれば、それは「胸先とブラのカップの縁を結んだ直線」と「胸先から胸表面に接するように引いた接線」が一致する時であることがわかります。その条件を境にして、（その条件よりさらに）胸とブラジャーの間に隙間がある場合に、ブラと胸の隙間を介して、胸先が見えてしまうことになる！ということになります。

　そこまでわかれば、後はとても簡単です。 下図のように「胸先とブラのカップの縁を結んだ直線」と「胸先から胸表面に接するように引いた接線」が一致した「胸先チラリ現象が生じる・生じないの境界線となる”胸先チラリのギリギリ条件”」状態の図を描き、胸の半径をr、3/4カップ形状ブラカップの半径をRとしてみれば、単純な補助線を描くことで、”胸先チラリのギリギリ条件”は、

ブラのカップ半径（R）＝半円状の胸の大きさ（半径 r） × 1 / Cos(22.5°)

となる時だということがわかります。つまり、ブラのカップサイズ（半径）が胸の大きさ（半径）の1 / Cos(22.5°)倍より大きくなってしまうと、胸先チラリ現象が生じてしまうというわけです。ちなみに、ここで登場する22.5°は、「3/4カップ形状のカット角＝45°」の半分です。

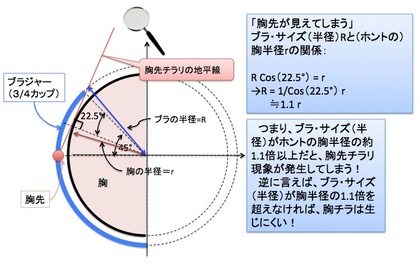
　1 / Cos(22.5°)は約1.1ですから、ブラのカップ・サイズ（半径）がホントの胸半径の約1.1倍より大きくなると、胸先チラリ現象が生じてしまう！ということになります。それは逆に言えば、ブラのカップ・サイズ（半径）がホントの胸半径の約1.1倍より小さければ、胸先が見えてしまうことはない、というわけです。

　ここまで来れば、後はもう簡単です。「ブラのカップ・サイズ（半径）」に関する少しの豆知識を組み合わせると、さらにリアルな「ブラジャーの中にある胸先が見えてしまう条件、すなわちブラのカップ・サイズ（半径）がホントの胸半径の約1.1倍より大きくなるというのは、一体どんな状況下で起こりうるのか？」という具体的状況すらわかります。

　まず、下の表は、ブラのカップ名称（AカップとかBカップとか言うアレですね）とアンダーバスト次第で、ブラジャーのカップ半径（cm）がどの程度の長さになるかを例示してみたものです。 ちなみに、ブラのカップ半径は、（トップバストとアンダーバストの差で定まる）AカップとかBカップといったカップ名称（だけ）で決まるわけではありません。 たとえば、下の表で言えば、アンダーバスト75cmのAカップもアンダー65cmのCカップも、カップ半径は同じく9.3cmというわけです。

　ブラジャーの中にある胸先が見えてしまう条件、すなわちブラのカップ・サイズ（半径）がホントの胸半径の約1.1倍より大きくなるというのは、（ホントの胸サイズにジャストフィットなものに対して）少し大きめのブラを着けてしまっている、という状況です。つまり、アンダーバストやAカップとかいったカップサイズを１サイズ程度選び間違えてしまうことで、ブラと胸の間に隙間ができ、そしてブラのカップ・サイズ（半径）がホントの胸半径の約1.1倍より大きくなってしまった場合に、胸先がチラリ見えるようになってしまうわけです。

　ここで重要なことは、ブラジャーのカップ半径表を眺めれば、「１サイズ程度選び間違えてしまった時、ブラのカップ半径が（間違えなかったとした場合をホントの胸の大きさだと考えれば）ホントの胸半径の約1.1倍より大きくなってしまう」というのが発生しうるのは、赤枠で囲った場合のみだということです。赤枠で囲ったカップ・サイズの場合のみ、ブラが１サイズ大きくなると半径が1.1倍超大きくなってしまうのです（それ以外のカップ・サイズの場合は、１サイズ大きいものを選んでも、元の大きさの1.1倍ほどの半径にはならないのです）。

　つまり、具体的には、

• アンダー65cmのB,Cカップ
• アンダー70cmのA,Bカップ
• アンダー75cmのAカップ

にのみ、「胸先チラリ条件が発動する」というわけです。アンダー65cmのCカップというのは、かなりレアなパターンでしょうから、実際のところ「胸先がチラリ見えてしまいやすいのは、A,Bカップにほぼ限られる」と言っても良いだろう、ということになります。

　というわけで、今回は単純な算数（数学）を使い「胸先チラリ…」の幾何学を考えてみました。数学的に導き出された結果は、胸先チラリ条件が生じるのは「ほぼBカップ以下の小胸さんに限られる！」という「なるほど、確かにそうかも！」という答えでした。この豆知識、実用的でもなければ・誰かに披露すれば人気者になれる…わけではなさそうですが、とても面白いと思いませんか!?

　「何人が集まれば、同じ誕生日の人（たち）がいる確率が50％を超えるか?」という問題があります。 計算すると、その答えは「23人」となり、意外に少ない人数でも「同じ誕生日の人たちがいる確率が高い」ので、誕生日のパラドックスと言われたりします。計算自体は、

同じ誕生日の人たちがいる確率＝1-同じ誕生日の人たちがいない確率

なので、「同じ誕生日の人たちがいない確率」を誕生日が重ならない条件と考えれば、たとえば23人であれば

　　　　＝1 – 364/365 × 363/365 × 362/365 …× (365-23 + 1) / 365
　　　　＝0.50729723432398540723…

と計算することができて、その確率は５０パーセントを超えるというわけです（詳しくはたとえばこちら）。

　ところで、戦前の日本の月別出生率を眺めると、誕生日が１〜３月に集中していたことがわかります。たとえば、「1899年から2000年までの月別出生率」を見ると、「１月・２月・３月の出生率が他の月の1.5倍くらい高く」「一番出生率が少ない６月と比べると、１〜３月は２倍ほど高い」という具合になっています。（データが途切れてる箇所が太平洋戦争時です）

　さて問題です。このような誕生日が１〜３月の時期に集中していた戦前の日本で「誕生日のパラドックス」を考えてみると、つまり「何人が集まれば、同じ誕生日の人（たち）がいる確率が50％を超えるか?」を考えてみると、一体どんな答が出てくるでしょう？…真夏の夜に挑戦するのに丁度良い面白いパズルだと思いませんか？直感的には、何人いれば同じ誕生日の人たちがいる確率が５０％を超えると思いますか？

　何年も前、深夜TV番組ロケで、大きな送風機を抱えて、スカート姿に風をあてて、スカートがめくれやすい条件を調べる実験をしたことがあります。さまざまな種類のスカートに、（手で持った送風機で）さまざまな風のあて方をする…という実験を延々２時間以上しましたが、スカートを風でまくり上げるのは意外なほど難しいものでした。

　しかし、送風機の風でスカートをまくり上げるのが難しかったのは、風を横からあてていたからで、スカートの下から強風を送れば、もちろん一瞬でスカートは吹き上げられてしまいます。それはつまり、「下から風が吹くような場所」ではスカートが風でめくれやすい、ということです。スカートは、種類によって違いますが、およそ１００〜３５０グラム程度の重さです。そんな重さのスカートを持ち上げることができる程度の風が、スカートの下方向から吹けば、風によってスカートはめくれあがってしまうことになります。

　「下方向から風が吹く」場所として、地下鉄駅のホームに降りるエスカレータがあります。地下鉄のホームに列車が近づいてくる時には、駅に近づいてくる列車が空気を圧縮し・ホーム近くの気圧を高めるため、ホーム側から（上部フロアに向かう）階段・エスカレータ通路で、上部フロアに向かう風が吹きます（参考：地下鉄の風）。この「列車風」と呼ばれる風は、条件によって異なりますが、たとえば風速5m/s程度になることがあります。それでは、スカートの下方向から吹く風速 5m/s の風がスカートをめくり上げることができるのでしょうか？

　非粘性流体のエネルギー保存則であるベルヌｰイの定理を使うと、スカート下部から吹く風が「スカートを持ち上げようとする力」は、

空気の密度 × スカートに下部から風が吹き込む面積 × 風速 × 風速 / 2

で見積もることができます。空気の密度を1.13(kg/m^3)として、スカートに下部から風が吹き込む面積は（ヒップ90ｃｍの女性で見積もると）0.06(m^2)程度でしょう。そして、ホームに向かうエスカレータに吹く列車風が5(m/s)とすると、

「スカートを持ち上げようとする力」=1.13× 0.06 × 5 × 5 / 2 = 0.85 (N)

になります。0.85 (N = ニュートン)ということは、0.85 (N) / 0.98 = 0.86kg重＝86グラムのものを持ち上げるのと同じ大きさの力ということですから、重さ８６グラムのスカートであったなら、ホームに向かうエスカレータ通路に5m/sの列車風が吹くとスカートがめくれあがってしまう、ということになります。とはいえ、スカートの重さは、冒頭に書いたように１００〜３５０グラム程度ですから、重さ８６グラムのスカートは「素材が非常に薄く軽い特殊なスカート」ということになります。だから、普通のスカートであれば、この程度の風では、スカートがめくれる可能性は低いわけです。

　しかし、スカート女性がエスカレータを急いで電車に乗ろうと駆け下りていたりすると、話は大きく変わります。たとえば、女性がでエスカレータを駆け下りていて、下りエスカレータ速度と駆け下りる速度が加わり（下りの速度が）秒速1m程度になった場合には、この1m/sが風速（5m/s）に足し合わされることになり、

「スカートを持ち上げようとする力」=1.13 × 0.06 × (5+1) × (5+1) / 2 = 1.2 (N) = 0.12 kg重

となり、重さ120グラム程度の（結して珍しくはない）スカートがめくれあがってしまうようになるのです。

　ちなみに、空気の密度は「高気圧で気温が低くて湿度が低い」時に重くなります。たとえば、１気圧・気温40 ℃・湿度0%の空気の密度は1.13 kg/m^3ですが、気温が0°まで下がると、密度は1.29 kg/m^3になります。また、気圧が5%高くなれば密度も5%高くなります。…そうした条件がすべて加わると、つまり「涼しく晴れた高気圧の温度が低い朝の地下鉄駅で、下りのエスカレータを（遅刻をしまいと）ドジっ娘が駆け下りる」状況で計算すると、

「スカートを持ち上げようとする力」=1.29 × 0.06 × (5+1) × (5+1) / 2 × 1.05 = 1.5 (N) = 0.15 kg重

となり、重さ150グラム程度の平均的な薄手スカートがめくれあがってしまう！ということがわかるのです。

　さらに言えば、列車風は「上り・下りの両ホームに同時に列車が進入してきて、その列車がどちらも（その駅には止まらない）通過列車だった」という時に、最大風速を記録しそうです。ということは、駅に止まらない通過列車がある地下鉄副都心線の（大きくない）駅などが、エスカレータ通路にスカートがめくれやすい風が吹く「スカートめくれの危険スポット」ということになります。

　計算してみると色んなことがわかる！というわけで、今回は「風でめくれるスカート」を科学してみました。「涼しく晴れた朝の地下鉄駅をドジっ娘が走る」とスカートが必ずめくれる!?くらいの力が生じてしまうのです。